The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.
To solve the problem, we need to find the length of the supporting wire attached to the roadway 18 m from the middle of a uniformly loaded suspension bridge, where the cable hangs in the form of a parabola.
1. Understand the Setup:
- The roadway is 100 m long, so the midpoint is at 50 m.
- The longest wire (at the ends) is 30 m, and the shortest wire (at the midpoint) is 6 m.
2. Define the Parabola:
- Let the vertex of the parabola be at the origin (0,0).
- The equation of the parabola can be expressed as y=ax2.
- The length of the wire at the midpoint (x = 0) is 6 m, so y(0)=6.
- The length of the wire at the ends (x = ±50) is 30 m, so y(50)=30.
3. Find the Coefficient 'a':
- From the midpoint, we have y(0)=6, which gives us 0=a(0)2+6 (this confirms the vertex).
- From the ends, we have y(50)=30:
30=a(50)2+6
30−6=2500a
24=2500a⟹a=242500=121250=6625
4. Equation of the Parabola:
- The equation of the parabola is:
y=6625x2+6
5. Calculate the Length of the Supporting Wire at 18 m from the Middle:
- The position 18 m from the middle is x=18.
- Substitute x=18 into the parabola's equation:
y(18)=6625(18)2+6
=6625⋅324+6
=1944625+6
=1944625+3750625=5944625
6. Length of the Supporting Wire:
- The length of the supporting wire at this point is the vertical distance from the roadway to the cable:
Length=y(18)=5944625≈9.51 m
Final Answer:
The length of the supporting wire attached to the roadway 18 m from the middle is approximately 9.51 m.
- The roadway is 100 m long, so the midpoint is at 50 m.
- The longest wire (at the ends) is 30 m, and the shortest wire (at the midpoint) is 6 m.
- Let the vertex of the parabola be at the origin (0,0).
- The equation of the parabola can be expressed as y=ax2.
- The length of the wire at the midpoint (x = 0) is 6 m, so y(0)=6.
- The length of the wire at the ends (x = ±50) is 30 m, so y(50)=30.
- From the midpoint, we have y(0)=6, which gives us 0=a(0)2+6 (this confirms the vertex).
- From the ends, we have y(50)=30:
30=a(50)2+6
30−6=2500a
24=2500a⟹a=242500=121250=6625
- The equation of the parabola is:
y=6625x2+6
- The position 18 m from the middle is x=18.
- Substitute x=18 into the parabola's equation:
y(18)=6625(18)2+6
=6625⋅324+6
=1944625+6
=1944625+3750625=5944625
- The length of the supporting wire at this point is the vertical distance from the roadway to the cable:
Length=y(18)=5944625≈9.51 m
The length of the supporting wire attached to the roadway 18 m from the middle is approximately 9.51 m.
Topper's Solved these Questions
- CONIC SECTIONSBOOK - NCERTCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.1
15 Videos
- CONIC SECTIONSBOOK - NCERTCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.2
12 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - NCERTCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - EXERCISE 5.4
6 Videos
- INTRODUCTION TO THREE DIMENSIONAL GEOMETRYBOOK - NCERTCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.1
4 Videos
Similar Questions
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100m long is supported by vertical wires attached to the cable, the longest wire being 30m and the shortest being 6m. Find the length of the supporting wire attached to the roadway 18m from the middle.
View Solutionover the towers of a bridge a cable is hung in the form of a parabola, have their tops 30 meters above the road way are 200 meters apart. If the cable is 5 meters above the road way at the centre of the bridge, then the length of the vertical supporting cable 30 meters from the centre is
View Solution
Knowledge Check
A metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
AThe loss in gravitational potential energy of mass M is Mgl.BThe elastic potential energy stored in the wire is MglCThe elastic potential energy stored in the wire is 12MglDHeat produced is loss of mechanical energy of system is 12MglA sphere of mass m attached with the free end of a steel wire of length l swings in the veritical plane form the horizontal positon.
Elongation of the wire in the vericle positon isAmglY(πr2)B2mglY(πr2)Cmgl3Y(πr2)D3mglY(πr2)
IF the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
View SolutionA horizontal wire 0⋅1m long having mass 3g carries a current of 5A. Find the magnitude of the magnetic field which must act 30∘ to the length of the wire inorder to support its weight.
View SolutionThe top of two vertical poles of height 20m and 14m are connected by a wire. If the wire makes an angle 30∘ with the horizontal, then the length of the wire is
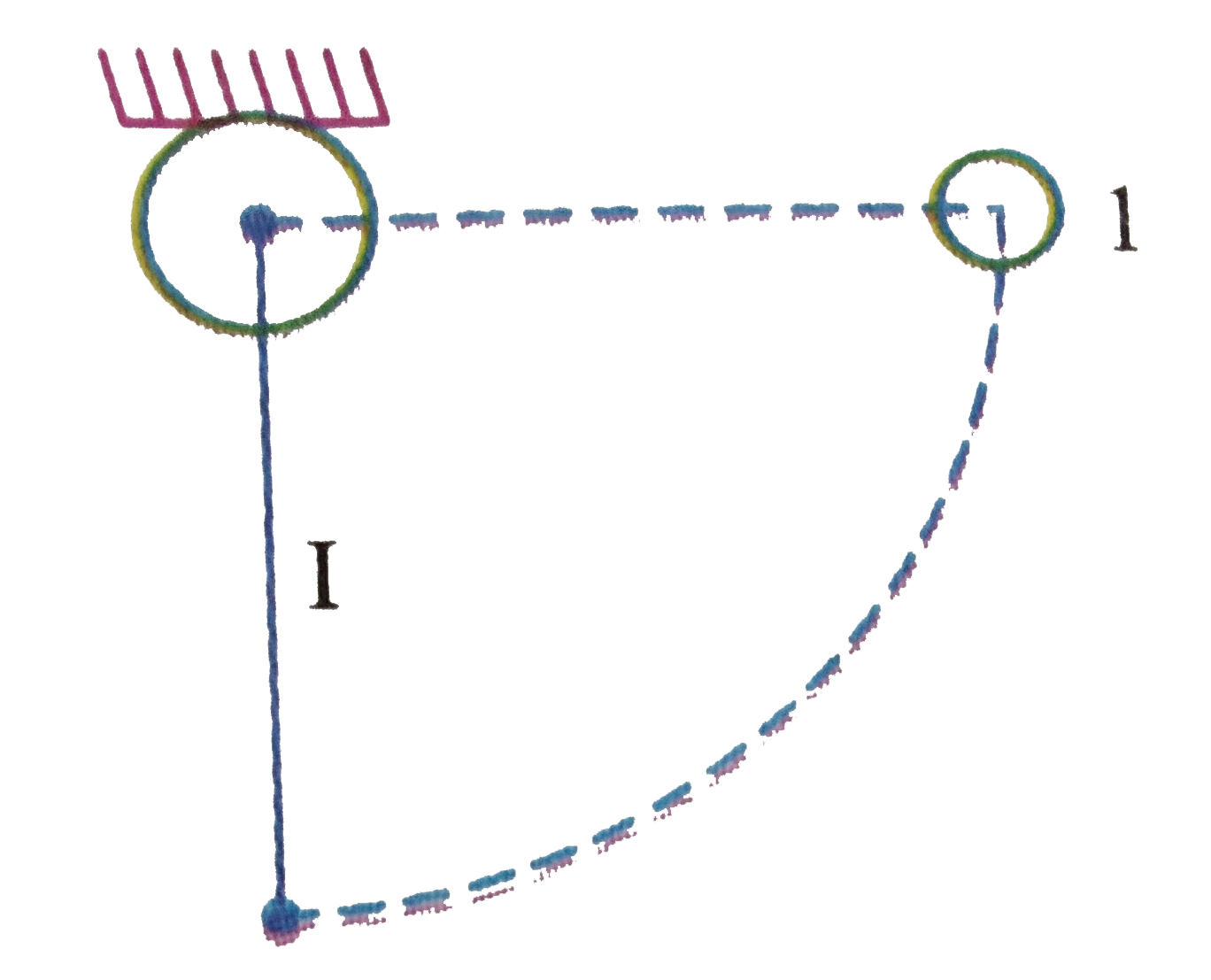
View SolutionA small mass m and its supporting wire because a simple pendulum when the horizontal cord is cut . Find the ratio of the tension in the supporting wire immediately after the cord is cut to the tension in the wire before the cord is cut
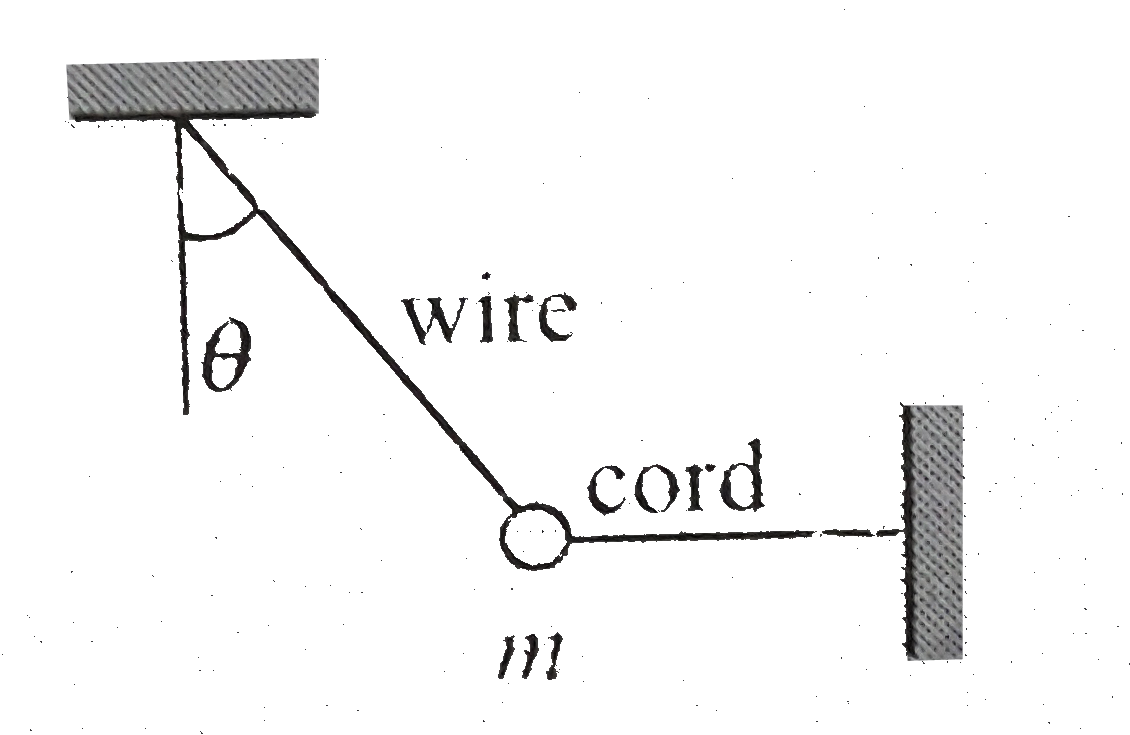
View SolutionThe diameter of a copper sphere is 18 cm. It is melted and drawn into a long wire of uniform cross section. If the length of the wire is 108 m, find its diameter.
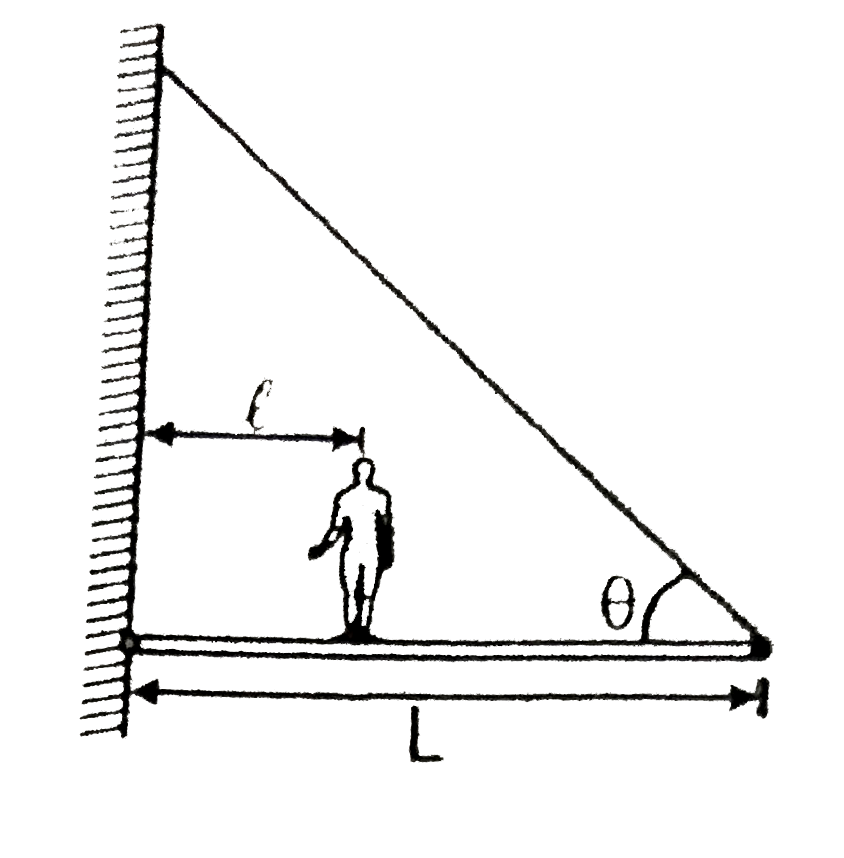
View SolutionA uniform horizontal beam of length L and mass M is attached to a wall by a pin connection. Its far end is supported by a cable that makes an angle θ with the horizontal . If a man of mass 'm' stands at a distance l from the wall , find the tension in the cable in equilibrium.
View Solution
