आयतन ABCD के अंदर स्थित O कोई बिन्दु है । सिद्ध कीजिए कि OB2+OD2=OA2+OC2 है ।
O से होकर जाती हुई PQ ।। BC खींची जिसमें P भुजा AB पर तथा Q भुजा DC पर स्थित हो ।
अब PQ||BC
अतः PQ⊥AB
तथा PQ⊥DC (∠B=90∘तथा∠C=90∘)
तब ∠BPQ=∠CQP=90∘ है |
अतः BPQC और APQD दोनों आयत हैं ।

ΔOPB से, OB2=BP2+OP2 . . . (1)
तथा ΔOQD से, OD2=OQ2+DQ2 . . . (2)
ΔOQC से, OC2=OQ2+CQ2 . . . (3)
ΔOAP से, OA2=AP2+OP2 . . . (4)
सम्बन्ध (1) तथा (2) को जोड़ने पर
OB2+OD2=BP2+OP2+OQ2+DQ2
=CQ2+OP2+OQ2−AP2
(क्योंकि BP = CQ तथा DQ = AP है )
=(CQ2+OQ2)+(OP2+AP2)
=OC2+OA2 [सम्बन्ध (3 ) तथा (4 ) से ]
अतः OB2+OD2=OC2+OA2.
Topper's Solved these Questions
- त्रिभुज Book:MANOHAR RAYChapter:त्रिभुज Exercise:उदाहरण
Explore 1 Video
- त्रिभुज Book:MANOHAR RAYChapter:त्रिभुज Exercise:प्रश्नावली 6(A)
Explore 2 Videos
- त्रिकोणमिति के कुछ अनुप्रयोगBook:MANOHAR RAYChapter:त्रिकोणमिति के कुछ अनुप्रयोगExercise:लघु उत्तरीय
Explore 2 Videos
- दो चार वाले रैखिक समीकरण युग्मBook:MANOHAR RAYChapter:दो चार वाले रैखिक समीकरण युग्मExercise:प्रश्नावली 3(I)
Explore 20 Videos
Similar Questions
निम्न आकृति में ∠P ज्ञात कीजिए ।

View Solutionनिम्नलिखित युग्मों के दो भिन्न - भिन्न उदाहरण दीजिए :
(i) समरूप आकृतियाँ
(ii) ऐसी आकृतियाँ जो समरूप नहीं हैं
View Solutionएक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधर : खड़ा हैं । टॉवर के ठीक सामने दूसरे के एक अन्य बिंदु से टॉवर शिखर का उन्नयन कोण 60∘ है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 30∘ है (देखिए आकृति) । टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए ।

View Solutionसमीकरण 8x+5y=11 को संतुष्ट करने वाले बिन्दु के निर्देशांक है :
View Solutionआयत ABCD के अंदर स्थित O कोई बिंदु है सिद्ध कीजिए कि OB2+OD2=OA2+OC2 है

View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
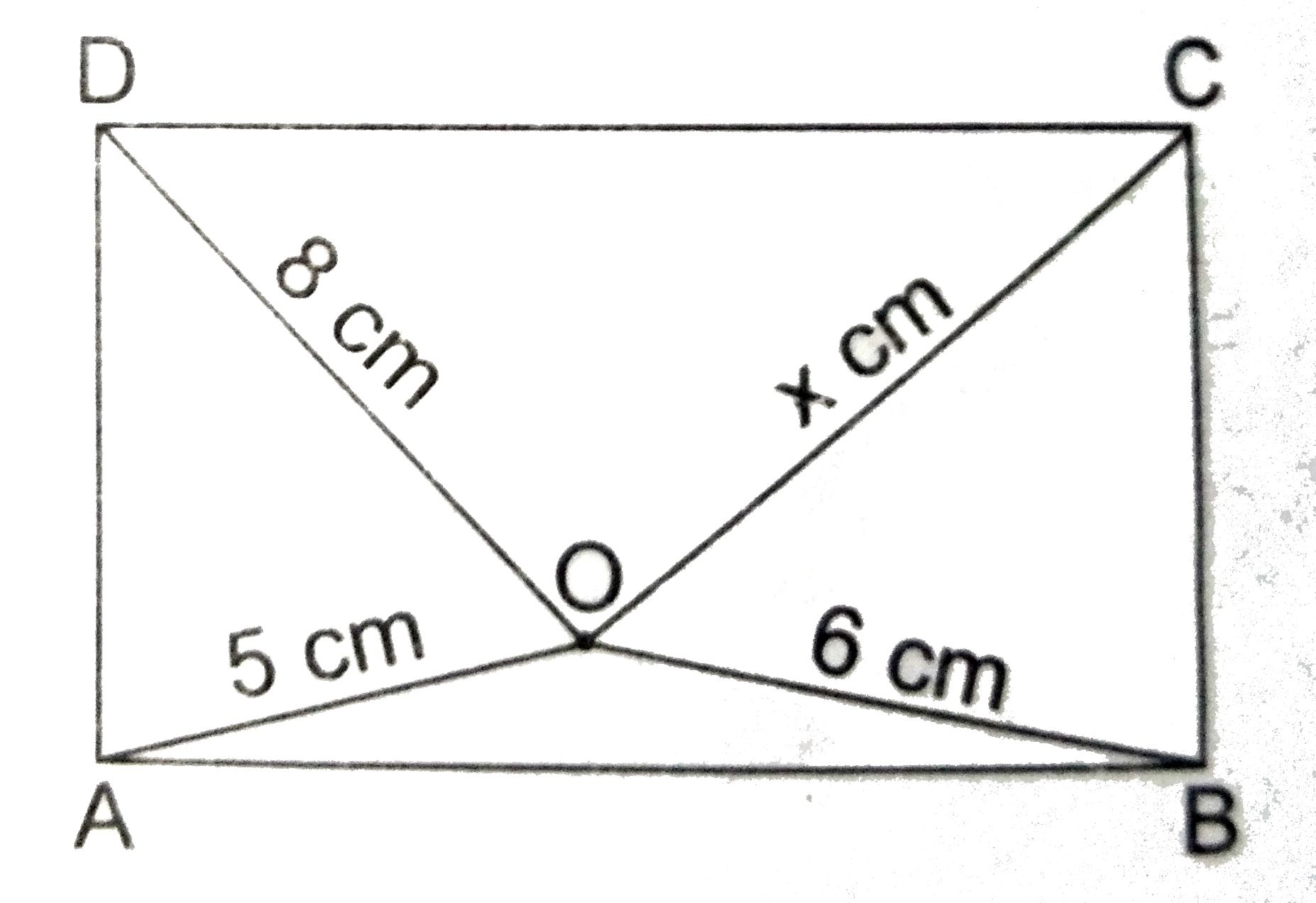
View SolutionO is any point inside a rectangle ABCD, Prove that OA2+OC2=OB2+OD2
View SolutionIn figure O is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
View SolutionO' is any point inside a rectangle ABCD.
Prove that OB2+OD2=OA2+OC2
View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View SolutionIf 'O' is any point in the interior of rectangle ABCD, then prove that : OB^(2) + OD^(2) = OA^(2) + OC^(2)
View Solutionபடத்தில் O என்பது செவ்வகம் ABCD யில் உள்ளே உள்ள எனில் ,OB2+OD2=OA2+OC2என நிரூபிக்க ?
View Solutionధీరగా చతురస్రం ABCD అంతరంలో ఏదైనా బిందువు 'O' అయితే OB2+OD2=OA2+OC2 అని చూపండి.
View Solution‘O’ is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2
View Solution

