Define principal axis of a spherical mirror.
A straight line passing through the pole and the centre of curvature of a spherical mirror is called its principal axis.
Topper's Solved these Questions
- SAMPLE QUESTION PAPER BOOK - X BOARDSCHAPTER - SAMPLE QUESTION PAPER EXERCISE - Section -B
11 Videos
- SAMPLE QUESTION PAPER BOOK - X BOARDSCHAPTER - SAMPLE QUESTION PAPER EXERCISE - Section -C
12 Videos
- QUESTION PAPER 2023BOOK - X BOARDSCHAPTER - QUESTION PAPER 2023EXERCISE - Question
16 Videos
- X BOARDSBOOK - X BOARDSCHAPTER - X BOARDSEXERCISE - SET III (SECTION -C)
1 Video
Similar Questions
Knowledge Check
A point object is placed on the principal axis of a spherical mirror. The object -distance u is
Adefinitely negativeBdefinitely positiveCpositive if the object is to the left of the centre of curvatureDpositive if the object is to the right of the centre of curvatureAB is the principal axis of a spherical mirror. I is the point image corresponding to a point object O. Choose the correct opritons.
 AMirror is lying to the right hand side of OBFocus of mirror is lying to the right hand side of OCCentre of curvature of mirror is lying to the right hand side of ODCentre of curvature of mirror is lying between I and O
AMirror is lying to the right hand side of OBFocus of mirror is lying to the right hand side of OCCentre of curvature of mirror is lying to the right hand side of ODCentre of curvature of mirror is lying between I and O
Mark the statement True (T) or False(F).A ray of light incident parallel to the principal axis of a spherical mirror retraces its path after reflection.
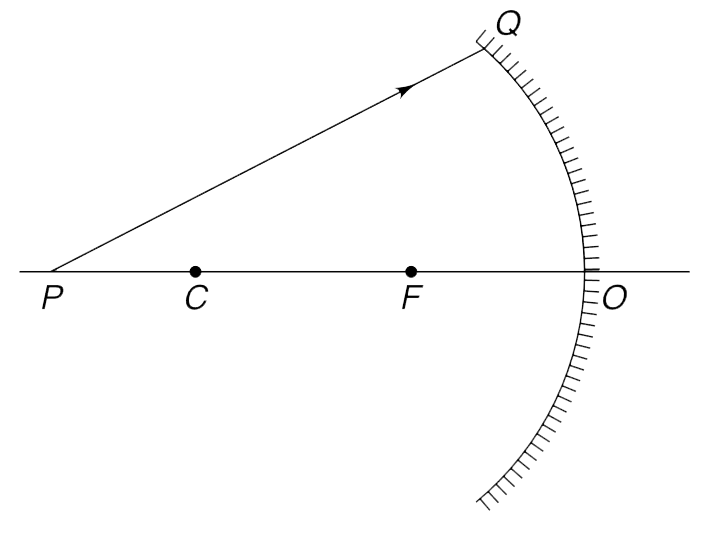
View SolutionWe know that parallel light rays which are inclined to the principal axis of a spherical mirror, after reflection converge at a point in the focal plane of the mirror. With this knowledge explain how you will trace the reflected ray for incident ray PQ shown in the Fig. F is focus and C is centre of curvature of the mirror.
View SolutionDefine the principal focus of a spherical mirror.
View SolutionA point light source lies on the principal axis of concave spherical mirror with radius of curvature 160 cm. Its image appears to be back of the mirror at a distance of 70 cm from mirror. Determine the location of the light source.
View SolutionSpherical Mirrors
View SolutionSpherical Mirrors
View Solution