A capacitor of capacitance 1μF is charged to potential 2 V and is connected to an inductor of 1 mH. At an instant when potential difference across. The capacitor is 1 V, the current in the circuit is 10−2√10x3 ampere. Find out the value of x.
The correct Answer is:9
To solve the problem, we will use the conservation of energy principle in an LC circuit, where the energy stored in the capacitor is equal to the sum of the energy stored in the capacitor and the inductor at any instant.
1. Identify Given Values:
- Capacitance, C=1μF=1×10−6F
- Initial Voltage across the capacitor, V0=2V
- Voltage across the capacitor at the instant of interest, V=1V
- Inductance, L=1mH=1×10−3H
- Current at that instant, I=10−2√10x3A
2. Calculate Initial Energy Stored in the Capacitor:
UC=12CV20=12×(1×10−6)×(22)=12×(1×10−6)×4=2×10−6J
3. Calculate Energy Stored in the Capacitor at the Instant:
U′C=12CV2=12×(1×10−6)×(12)=12×(1×10−6)×1=0.5×10−6J
4. Using Conservation of Energy:
The total energy initially stored in the capacitor is equal to the energy stored in the capacitor at the instant plus the energy stored in the inductor at that instant:
UC=U′C+UL
Where UL=12LI2.
5. Substituting Values:
2×10−6=0.5×10−6+12(1×10−3)I2
6. Rearranging to Find I2:
2×10−6−0.5×10−6=12(1×10−3)I2
1.5×10−6=12×10−3I2
1.5×10−6=0.5×10−3I2
I2=1.5×10−60.5×10−3=3×10−3
7. Substituting the Expression for Current:
I2=(10−2√10x3)2
3×10−3=10−410x3
3×10−3×3=10−4×10x
9×10−3=10−4×10x
9×10−3=10−3x
x=9
Final Answer:
The value of x is 9.
- Capacitance, C=1μF=1×10−6F
- Initial Voltage across the capacitor, V0=2V
- Voltage across the capacitor at the instant of interest, V=1V
- Inductance, L=1mH=1×10−3H
- Current at that instant, I=10−2√10x3A
UC=12CV20=12×(1×10−6)×(22)=12×(1×10−6)×4=2×10−6J
U′C=12CV2=12×(1×10−6)×(12)=12×(1×10−6)×1=0.5×10−6J
The total energy initially stored in the capacitor is equal to the energy stored in the capacitor at the instant plus the energy stored in the inductor at that instant:
UC=U′C+UL
Where UL=12LI2.
2×10−6=0.5×10−6+12(1×10−3)I2
2×10−6−0.5×10−6=12(1×10−3)I2
1.5×10−6=12×10−3I2
1.5×10−6=0.5×10−3I2
I2=1.5×10−60.5×10−3=3×10−3
I2=(10−2√10x3)2
3×10−3=10−410x3
3×10−3×3=10−4×10x
9×10−3=10−4×10x
9×10−3=10−3x
x=9
The value of x is 9.
Topper's Solved these Questions
- ALTERNATING CURRENT Book:AAKASH INSTITUTEChapter:ALTERNATING CURRENT Exercise:Assignment (Section-H) (Multiple True-False Type Questions)
Explore 2 Videos
- ALTERNATING CURRENT Book:AAKASH INSTITUTEChapter:ALTERNATING CURRENT Exercise:Assignment (Section-I )(subjective Type Questions)
Explore 1 Video
- ALTERNATING CURRENT Book:AAKASH INSTITUTEChapter:ALTERNATING CURRENT Exercise:Assignment (Section - F) (Matrix- Match Type Questions)
Explore 1 Video
- ATOMSBook:AAKASH INSTITUTEChapter:ATOMSExercise:ASSIGNMENT SECTION J (Aakash Challengers )
Explore 4 Videos
Similar Questions
In the circuit shown in the following the potential difference across the 3μF capacitor is
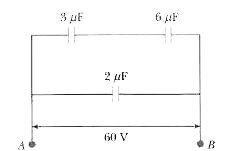
View SolutionA capacitor of capacitance 54μF is charged ot a potential of 25 V and then connected to a 15 mH inductor to produce oscillations. What was the energy stored in the capacitor initially and to what wavelength will the circuit respond ?
View Solution
Knowledge Check
A capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 0.2mH. At an instant when potential difference across the capacitor is 6v
Acurrent in the circuit is 1.04ABmagnetic energy in the magnetic field is 108μJCcurrent in the circuit is 1.04ADangular frequency of the circuit is 5×104radsA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1A capasitor of capacitance 1(μ)F is charged to a potential of 1 V, it is connected in parallel to an inductor of inductance 10−3H. The maximum current that will flow in the circuit has the value
A(A) √1000mAB(B) 1mAC(C) 1(μ)AD(D) 1000mA
A capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionA capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 6μH. What is the current (in A) in the circuit at a time when the potential difference across the capacitor is 6.0V?
View SolutionA parallel plate capacitor of capacitance 1μF has a charge of +2μC on one of the plates and a charge of +4μC on the other. The potential difference developed across the capacitor is
View SolutionTwo capacitors of capacitances 10μFand20μF are connected in series across a potential difference of 100V. The potential difference across each capacitor is respectively
View SolutionA capacitor of capacitance 10μF charged to 100V is connected to an uncharged capacitor. The effective potential now is 40 V. The capacitance on uncharged capacitor is
View Solution

