A dust particle lying at the rim of a wheel has an angular speed of 22 rad/s. Find the time period.
The correct Answer is:27s
To find the time period of a dust particle lying at the rim of a wheel with an angular speed of 22 rad/s, we can follow these steps:
Step 1: Understand the relationship between angular speed and time period
The angular speed (ω) is related to the time period (T) by the formula:
T=2πω
where:
- T is the time period,
- ω is the angular speed in radians per second.
Step 2: Substitute the given value of angular speed
We are given that the angular speed ω is 22 rad/s. We will substitute this value into the formula:
T=2π22
Step 3: Simplify the expression
Now, we can simplify the expression:
T=2π22=π11 seconds
Step 4: Calculate the numerical value
To get a numerical value, we can use the approximation π≈3.14:
T≈3.1411≈0.285 seconds
Final Answer
Thus, the time period of the dust particle is approximately:
T≈0.285 seconds
---
The angular speed (ω) is related to the time period (T) by the formula:
T=2πω
where:
- T is the time period,
- ω is the angular speed in radians per second.
We are given that the angular speed ω is 22 rad/s. We will substitute this value into the formula:
T=2π22
Now, we can simplify the expression:
T=2π22=π11 seconds
To get a numerical value, we can use the approximation π≈3.14:
T≈3.1411≈0.285 seconds
Thus, the time period of the dust particle is approximately:
T≈0.285 seconds
Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Assignement section -A Objective (one option is correct)
Explore 50 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Assignement section -B Objective (one option is correct)
Explore 24 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:llustration 1 :
Explore 1 Video
- MOCK_TEST_17Book:AAKASH INSTITUTEChapter:MOCK_TEST_17Exercise:Example
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
Similar Questions
A disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of a radius.
View SolutionA particle is revolving in a circle of radius 1 m with an angular speed of 12 rad/s. At t = 0, it was subjected to a constant angular acceleration α and its angular speed increased to (480π) rotation per minute (rpm) in 2 sec. Particle then continues to move with attained speed. Calculate
(i) angular acceleration of the particle,
(ii) tangential velocity of the particle as a function of time.
(iii) acceleration of the particle at t = 0.5 second and at t = 3 second
(iv) angular displacement at t = 3 second.
View Solution
Knowledge Check
Two people start at the same place and walk around a circular lake in opposite directions. One has an angular speed of 1.7×10−3 rad/s while the other has an angular speed of 3.4×10−3 rad/s. How long will it be before they meet?
A600 sB2400 sC1231 sD1800 sAfter 10.0 s, a spinning roulette wheel at a casino has slowed down to an angular velocity of +1.88 rad/s. During this time, the wheel has an angular acceleration of −5.04rad/s2. Determine the angular displacement of the wheel.
A+440 radB+252 radC+271 radD+188 radA wheel has angular acceleration of 3.0 rad/sec2 and an initial angular speed of 2.00 rad/sec. In a time of 2 sec it has rotated through an angle (in radian) of
A10B12C4D6
A wheel of radius 15cm is rotating about its axis at angluar speed of 20rad/s. Find the linear speed and total acceleration of a point on the rim.
View SolutionA simple pendulum of length 40 cm oscillates with an angular amplitude of 0.04 rad. Find a. the time period b. the linear amplitude of the bob, c. The speed of the bob when the strig makes 0.02 rad with the vertical and d. the angular acceleration when the bob is in moemntary rest. Take g=10ms−2.
View SolutionTwo particles AandB move on a circle Initially, particles AandB are diagonally opposite to each other. Particle A moves with angular velocity πrads−1 and angular acceleration π/2rads−2 and particle B moves with constant angular velocity 2πrads−2. Find the time after which both the particlsd AnadB will collide.
View SolutionThree particles are connected by light, right rods lying along the y-axis. If the system rotates about the x-axis with an angular speed of 2 rad/s, the M.I. of the system is
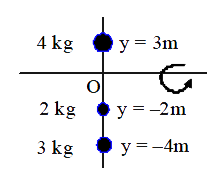
View SolutionA particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
View Solution

