If $α, β, γ$ are the angles which a line makes with positive direction of the axes, then match the quantities in
Column-I to their values in column-II :

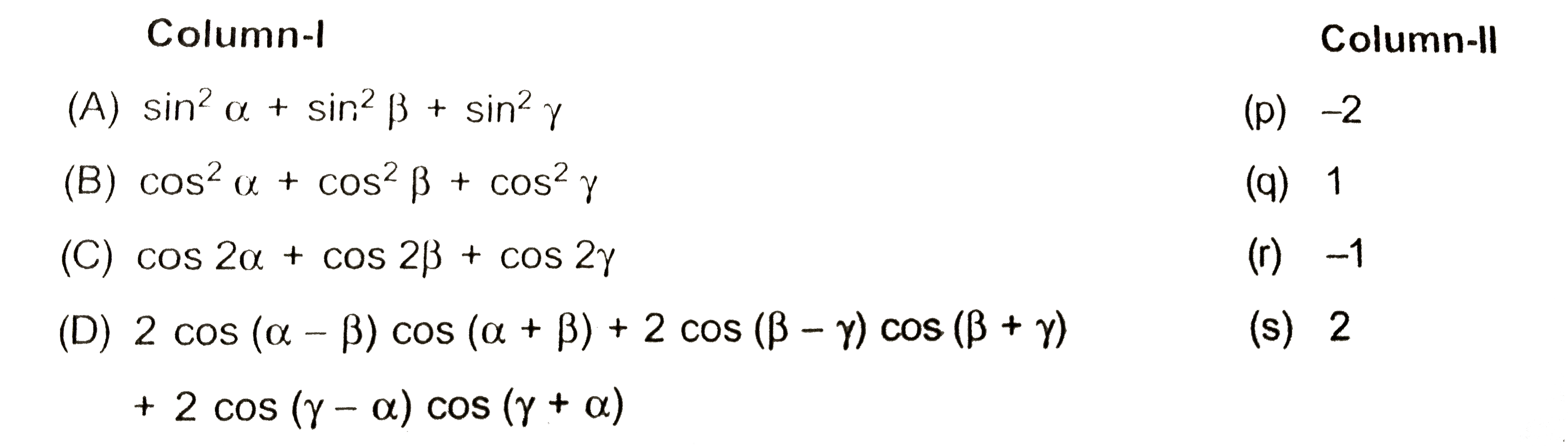
Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - G
7videos
THREE DIMENSIONAL GEOMETRY
BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - H
4videos
THREE DIMENSIONAL GEOMETRY
BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - E
9videos
THREE DIMENSIONAL GEOMETRY
BOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
5videos
STRAIGHT LINES
BOOK - AAKASH INSTITUTECHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
15videos
TRIGNOMETRIC FUNCTIONS

Similar Questions

Knowledge Check

Question 1 - Select One
If $α, β, γ$ be the angles which a line makes with the coordinates axes, then
A ${sin}^{2} α + {sin}^{2} β + {sin}^{2} γ = 1$
B ${sin}^{2} α + {sin}^{2} β + {sin}^{2} γ = 1$
C ${cos}^{2} α + {cos}^{2} β + {cos}^{2} γ = 1$
D ${cos}^{2} α + {sin}^{2} β + {sin}^{2} γ = 1$
Question 2 - Select One
If $α, β, γ$ be angles which a straighat line makes with the positive direction of the axes, then ${sin}^{2} α + {sin}^{2} β + {sin}^{2} γ$ is equal to (A) 4 (B) 1 (C) 2 (D) 3
A2
B3
C4
DNone
Question 3 - Select One
If $α, β, γ$ are direction angles of a line, then
A $0 \leq α, β, γ \leq \frac{π}{2}$
B $0 \leq α, β, γ \leq π$
C $0 < α, β, γ < \frac{π}{2}$
D $0 < α, β, γ < π$

AAKASH INSTITUTE-THREE DIMENSIONAL GEOMETRY -ASSIGNMENT SECTION - F

Home
Ask Doubt
Profile