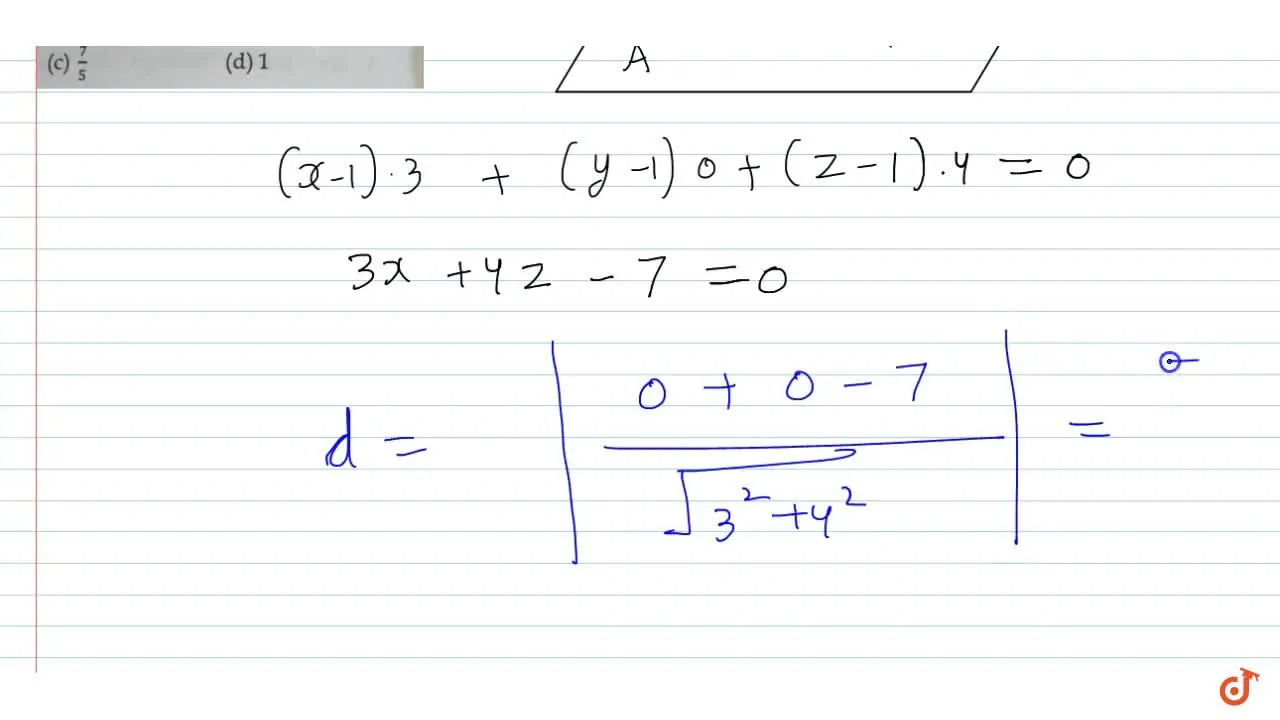If plane passes through the point (1, 1,1) and is perpendicular to the line,, then its perpendicular distance from the origin is
1
The correct Answer is:C
Step by step video, text & image solution for If plane passes through the point (1, 1,1) and is perpendicular to the line,(x-1)/3=(y-1)/0=(z-1)/4, then its perpendicular distance from the origin is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - B47videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - C14videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - TRY YOURSELF97videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)5videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTECHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)15videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
If a plane passes through the point (1, 1, 1) and is perpendicular to the line x−13=y−10=z−14, then its perpendicular distance from the origin is -
View SolutionIf a plane passes through the point (1,1,1) and is perpendicular to the line x−13=y−10=z−14, then its perpendicular distance from the origin is -
View SolutionThe equation of a plane through the point A(1,0,-1) and perpendicular to the line x+12=y+34=z+7−3 is
View SolutionThe equation of the line through the point (0,1,2) and perpendicular to the line x−12=y+13=z−1−2 is :
View SolutionThe plane passing through the point (5,1,2) perpendicular to the line 2(x−2)=y−4=z−5 will meet the line in the point :
View SolutionThe equation of the line passing through the point (1,2) and perpendicular to the line x+y+1=0 is
View SolutionFind the equation of the plane passing through the point (1,2,1) and perpendicular to the line joining the points (1,4,2)and(2,3,5). find also the perpendicular distance of the origin from this plane.
View SolutionThe line passing through the point -1, 2, 3 and perpendicular to the plane x - 2y + 3z + 5 = 0 will be
View SolutionThe equation of the line passing though the point (1,1,−1) and perpendicular to the plane x−2y−3z=7 is :
View SolutionEquation of plane passing through two points (-1,2,0), (1,1,2) and perpendicular to the plane x+2y+2z=4 is
View Solution