The plane xa+yb+zc=1 meets the co-ordinate axes in the point A, B, C respectively. Find the
area △ABC.
Video Solution
Text Solution
Let the given plane xa+yb+zc= meet the coordinate axes in the point A,(a, 0, 0), B(0, b, 0) and C(0, 0, c).
Let △xy,△yz,△zx be the projection of the area of trangle
ABC on x−y,y−zandz−xplane. Then
△2=△2xy+△2yz+△2zx
Now △xy=12[a(b−0)+0(0−0)+0]=ab2
Similarly △yz=12bcand△zx=12ca.
Hence △2=△2xy+△2yz+△2zx=14(a2b2+b2c2+c2a2)
⇒△=12√a2b2+b2c2+c2a2.
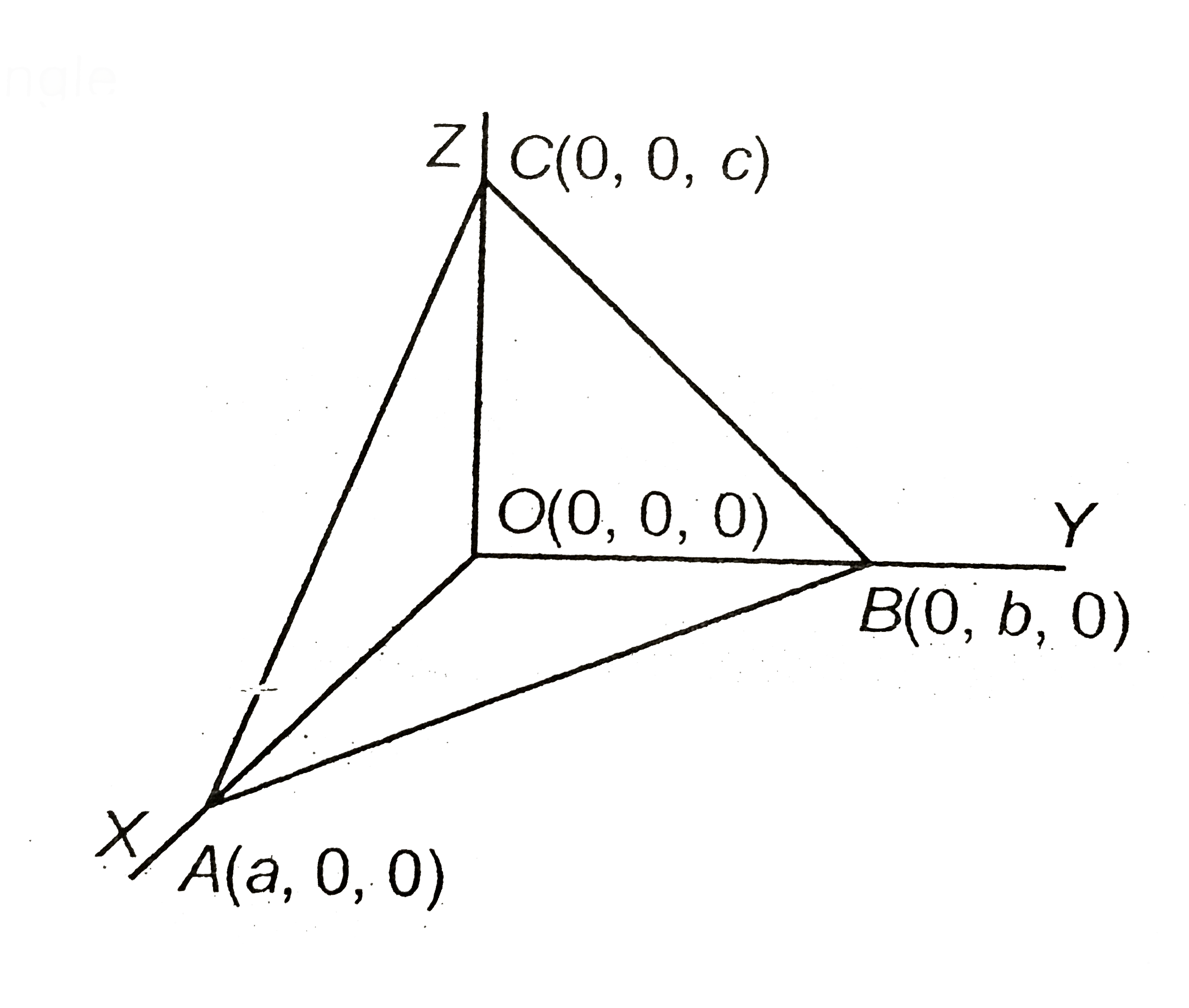
|
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - Illustration
4 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - TRY YOURSELF
97 Videos
- STRAIGHT LINESBOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
5 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTECHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
15 Videos
Similar Questions
Knowledge Check
The plane xa+yb+zc=1 meets the coordinate axes at A,B and C respectively. Find the equation of the sphere OABC.
Ax2+y2+z2+ax+by+cz=0Bx2+y2+z2−ax+by+cz=0Cx2+y2+z2+2ax+2by+2cz=0Dx2+y2+z2−2ax+2by+2cz=0If the plane x1+y2+z3=1 meets the co-ordinate axes in the points A, B and C, then area of △ABC in sq. units is
A32B52C72D92If the planes ax+by + cz=1 meets the co-ordinates axes in the points A,B,C, then the centroid of △ABCis
A(3a,3b,3c)B(a3,b3,c3)C(3a,3b,3c)D(13a,13b,13c)
The plane ax+by+cz=1 meets the coordinate axes in A,B,C. The centroid of ΔABC is
View SolutionIf the plane xa+yb+zc=1 meets the axes in A, B, C respectively. Find the equation of a sphere OABC.
View SolutionIf the plane x2+y3+z6=1 cuts the coordinates axes at points A,B and C. Then, find the area of △ ABC.
View SolutionIf the planes ax+by + cz=1 meets the co-ordinates axes in the points A,B,C, then the centroid of △ABCis
View SolutionThe plane xa+yb+zc=3 meets the co-ordinate axes in A,B,C. The centroid of the triangle ABC is
View Solution