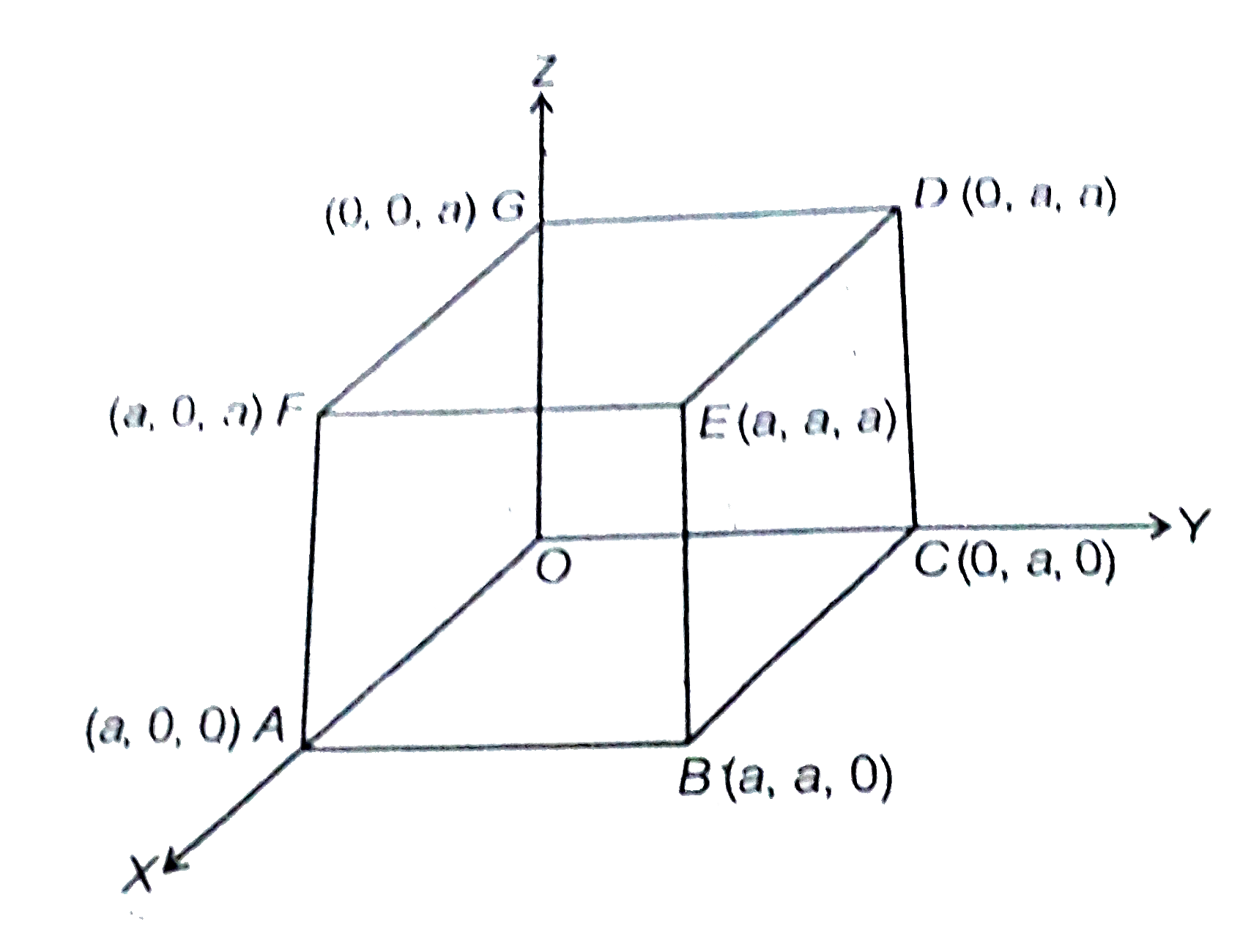
A line makes angles $α, β, γ$ and $δ$ with the diagonals of a cube, prove that $\cos^{2} α + \cos^{2} β + \cos^{2} γ + \cos^{2} δ = \frac{4}{3}$

Video Solution

Text Solution

Verified by Experts

Angle between two lines is geven by
$\cos θ = \frac{{\vec{b}}_{1} \cdot {\vec{b}}_{2}}{| {\vec{b}}_{1} | | {\vec{b}}_{2} |} ({\vec{b}}_{1} and {\vec{b}}_{2}$ are parallel vectors to given lines)
Four diagonals of cube are OE, AD, BG and ltbtgt OE is parallel to $a (i + j + K)$
AD is parallel to $a (- \hat{i} + \hat{j} + \hat{k})$
BG is parallel to $a (- \hat{i} - \hat{j} + \hat{k})$
CF is parallel to $a (\hat{i} - \hat{j} + \hat{k})$
Let the equation of given line is
$\vec{r} = λ (l \hat{i} + m \hat{j} + n \hat{k})$ (l, m, n, are direction cosines)
angle between $\vec{O E}$ and given line
$\cos α = \frac{a (l + m + n)}{\sqrt{3} a \times 1} \dots (i)$
angle between $\vec{A D}$ and given line
$\cos β = \frac{a (- l + m + n)}{\sqrt{3} a} \dots (i i)$
angle between $\vec{B G}$ and given line
$\cos γ = \frac{a (- l - m + n)}{\sqrt{3} a} \dots (i i i)$
angal between $\vec{C F}$ and give line
$\cos δ = \frac{a (l + m + n)}{\sqrt{3} a} \dots (i v)$
Squaring and adding (i), (ii), (iii) and (iv)
$\cos^{2} α + \cos^{2} β + \cos^{2} γ + \cos^{2} δ = \frac{{(l + m + n)}^{2} + {(- l + m + n)}^{2} + {(- l - m + n)}^{2} + {(l - m + n)}^{2}}{3}$
$= \frac{4}{3} (l^{2} + m^{2} + n^{2}) = \frac{4}{3}$

Updated on:21/07/2023

A line makes angles $α, β, γ a n d δ$ with the diagonals of a cube. Show that ${cos}^{2} α + {cos}^{2} β + {cos}^{2} γ + {cos}^{2} δ = 4 / 3 .$
A $\frac{1}{2}$
B $\frac{1}{4}$
C $\frac{3}{4}$
D $\frac{4}{3}$
A line makes angles $α, β, γ a n d δ$ with the diagonals of a cube. Show that ${cos}^{2} α + {cos}^{2} β + {cos}^{2} γ + {cos}^{2} δ = 4 / 3 .$
A $\frac{2}{3}$
B $\frac{4}{3}$
C $\frac{8}{3}$
D1
A line makes an angle $α, β, γ, δ$ with the four diagonals of a cube, then ${sin}^{2} α + {sin}^{2} β + {sin}^{2} γ + {sin}^{2} δ =$
A $\frac{4}{3}$
B $\frac{8}{3}$
C $\frac{1}{3}$
D $\frac{2}{3}$