Show that the coordinates off the centroid of the triangle with vertices A(x1,y1,z1), B(x2,y2,z2)and (x3,y3,z3) are (x1+x2+x33,y1+y2+y33,z1+z2+z33)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Suppose D is the mid-point of BC. Then coordinates of D are
(x2+x32,y2+y32,z2+z32)
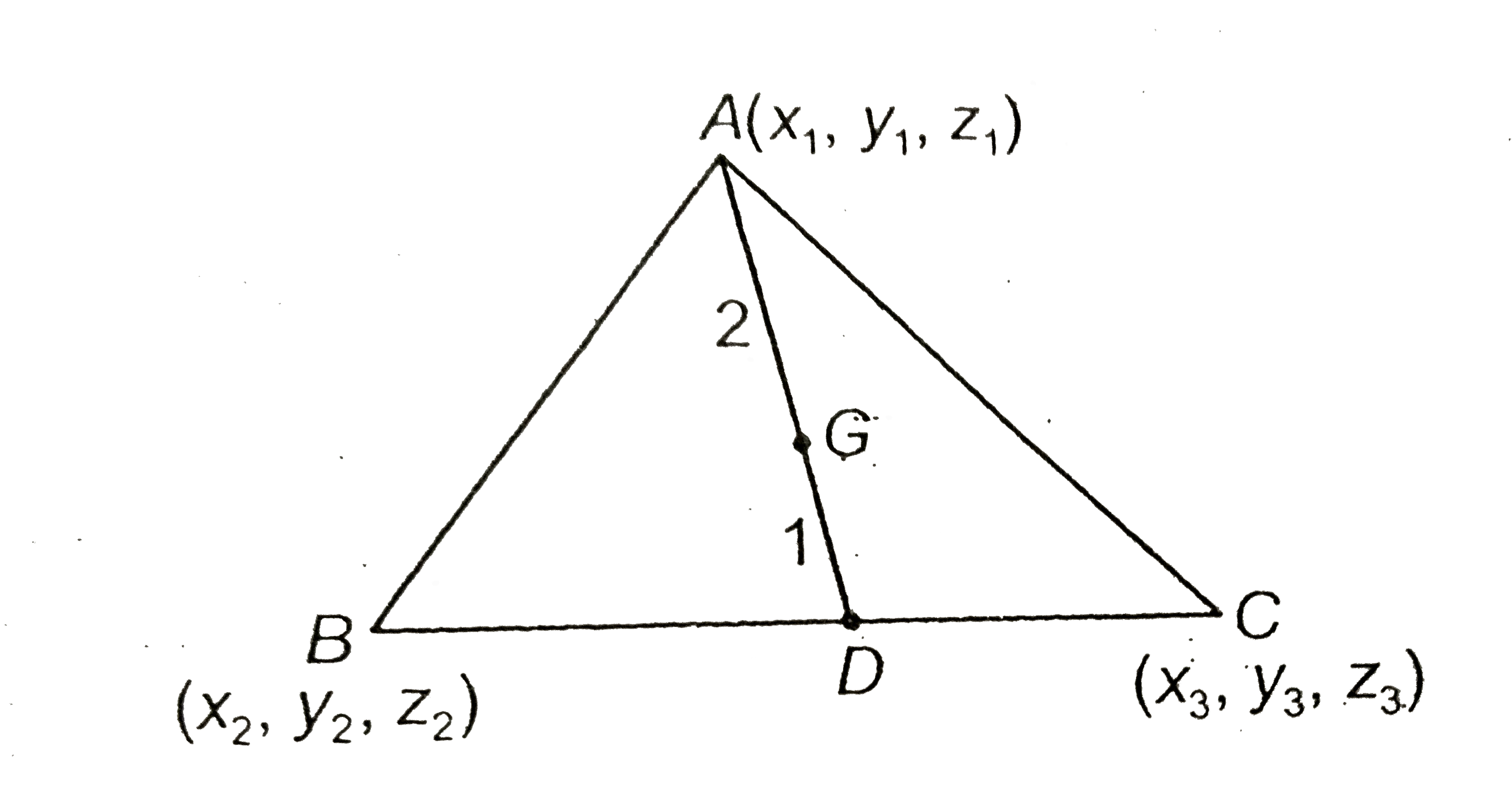
ocr_image
Let G the centroid of △ABC. Then G divides AD in the ratio 2 : 1.
Hence, coordinates of G are
∴⎛⎜ ⎜⎝1⋅x1+2(x2+x32)1+2,1⋅y+2(y2+y32)1+2,1⋅z1+2(z2+z32)1+2⎞⎟ ⎟⎠
=(x1+x2+x33,y1+y2+y33,z1+z2+z33)

Updated on:21/07/2023
|
Class 12MATHSTHREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • STATEMENT-1 : The centroid of a tetrahedron with vertices (0, 0,0), (4, 0, 0), (0, -8, 0), (0, 0, 12)is (1, -2, 3).
    and
    STATEMENT-2 : The centroid of a triangle with vertices (x1,y1,z1),(x2,y2,z2)and(x3,y3,z3) is
    (x1+x2+x33,y1+y2+y33,z1+z2+z33)

    AStatement-1 is True, Statement-2 is true, Statement- is a correct explanation for Statement -1
    BStatement-1 is True, Statement-2 is true, Statement- is NOT a correct explanation for Statement -1
    CStatement-1 is True, Statement-2 is False
    DStatement-1 is False, Statement-2 is true

  • If Δ=∣∣ ∣ ∣∣x1+iy1x1i−y1z1x2+iy2x2i−y2z2x3+iy3x3i−y3z3∣∣ ∣ ∣∣ then Δ is

    A−1
    B2i
    C0
    D3i

  • The equation of the plane passing through A(x1,y1,z1) and containg the line x=x2d1=y=y2d2=z=z2d3 is

    A∣∣ ∣ ∣∣x+x1y+y1z+z1x2+x1y2+y1z2+z1d1d2d3∣∣ ∣ ∣∣=0
    B∣∣ ∣ ∣∣x−x1y−y1z−z1x2−x1y2−y1z2−z1d1d2d3∣∣ ∣ ∣∣=0
    C∣∣ ∣ ∣∣x−d1y−d2z−d3x1y1z1x2y2z2∣∣ ∣ ∣∣=0
    D∣∣ ∣ ∣∣xyzx1−x2y1−y2z1−z2d1d2d2∣∣ ∣ ∣∣=0