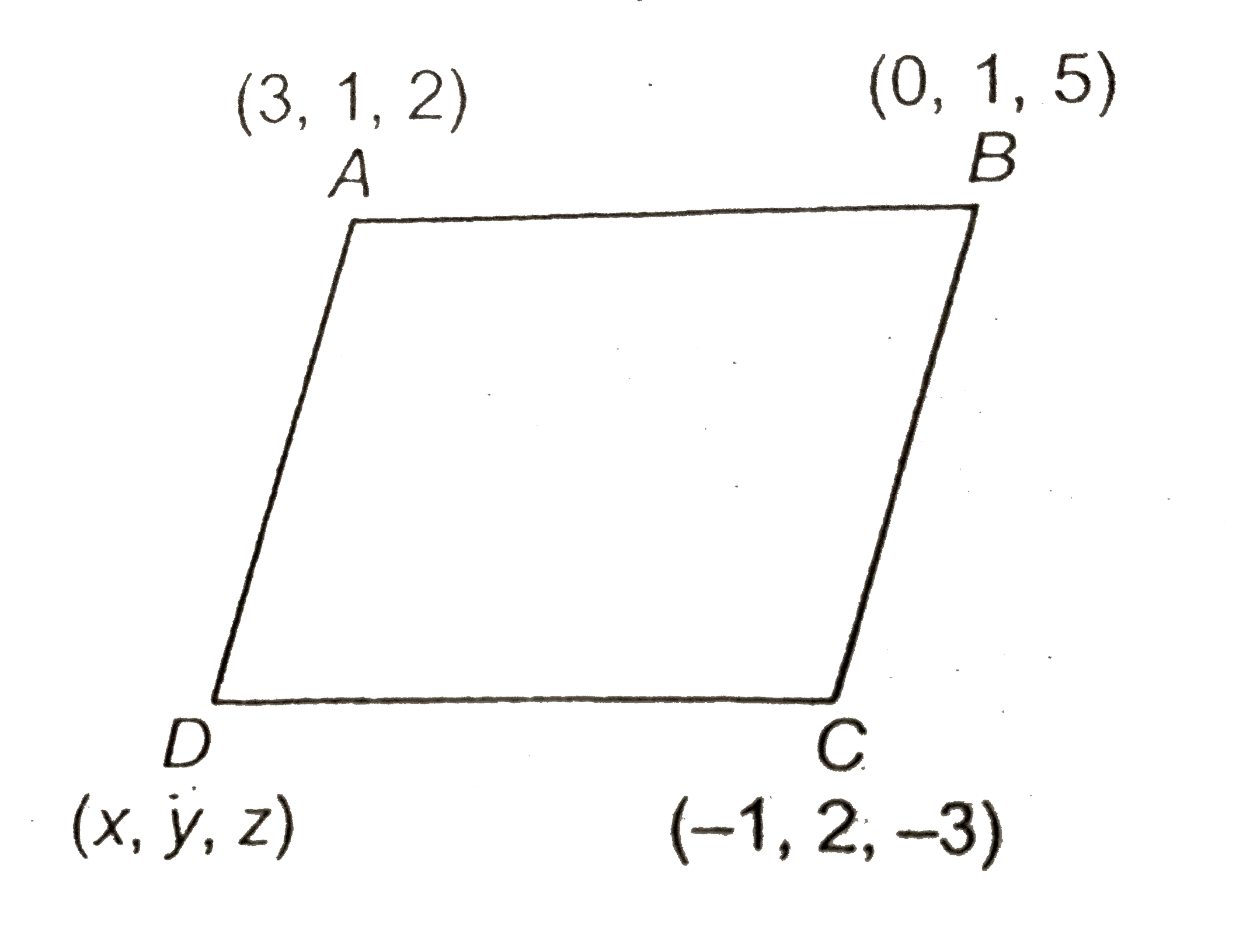
Three vertices of a parallelogram ABCD are A(3, 1, 2), B(0, 1, 5) and C(-1, 2, -3) Find the
coordinates of the fourth vertex.
Let the coordinates of the fourth vertex D be (x, y, z)
Since diagonals of a parallelogram bisect each other. Therefore, mid-point of AC and BD coincide.
∴(3−12,1+22,2−32)=(0+x2,y+12,z+52)
⇒(1,32,−12)=(x2,y+12,z+52)
⇒x2=1,y+12=32,z+52=_12
⇒x=2,y=2andz=−6
Hence the coordinates of the fouth vertex are (2, 2, -6).
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - Illustration
4 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - TRY YOURSELF
97 Videos
- STRAIGHT LINESBOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
5 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTECHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
15 Videos
Similar Questions
Knowledge Check
If the three vertices of a parallelogram ABCD are
A(3, -1, 5), B(1, -2, -4) and C(0, 3, 0), then the
coordinates of fourth vertex isA(2, 4, 9)B(2, -4, -9)C(0, 4, 9)D(0, -4, -9)The co-ordinates of three vertices of a parallelogram ABCD are A(1,0) , B(3,4) and C(1,2). The co-ordinates of fourth vertex D are :
A(−1,2)B(−5,−4)C(1,2)D(2,0)
The co-ordinates of the vertices of a parallelogram ABCD are A(-1,2,3), B(2, -4,1) and C(1,2,-1). Find the co-ordinates of its 4th vertex.
View SolutionThree vertices of a parallelogram are (1, 2, 1), (2, 5, 6) and (1, 6, 0) Find the coordinates of
the fourth vertex.
View SolutionThree vertices of a parallelogram are (0, 0, 0), (2, -1, 2) and (5, 6, 8) Find the coordinates of
the Fourth vertex.
View SolutionThe coordinates of three consecutive vertices of a parallelogram are (1, 3), (-1, 2) and (2, 5). Then find the coordinates of the fourth vertex.
View SolutionThe three vertices of a parallelogram ABCD taken in order are A(3, -4), B(-1, -3) and C(-6, 2). Find the coordinates of the fourth vertex D.
View SolutionThe three vertices of a parallelogram ABCD are A(-1,3,4), B(2,-1,3) and C(5,1,2). Find the co-ordinates of its 4th vertex D.
View Solution