If a ladder which is 10m long rests against a vertical wall. If the base of ladder slides away from the wall at 1 m/s then how fast is the top of the ladder sliding down along the wall when the base is 6 m from the wall ?
Let at any instant end points of ladder is at point P(a,0) and Q(0,b) .
Length of ladder = 10 hence a2+b2=100
Differentiate w.r.t.
2adadt+2bdbdt=0
Given that , dadt= 1m/s when a=6m, b=8 m
6×1+8dbdt=0
dbdt=−34 m/s
So, top of the ladder will be sliding down at a rate of 34m/s .
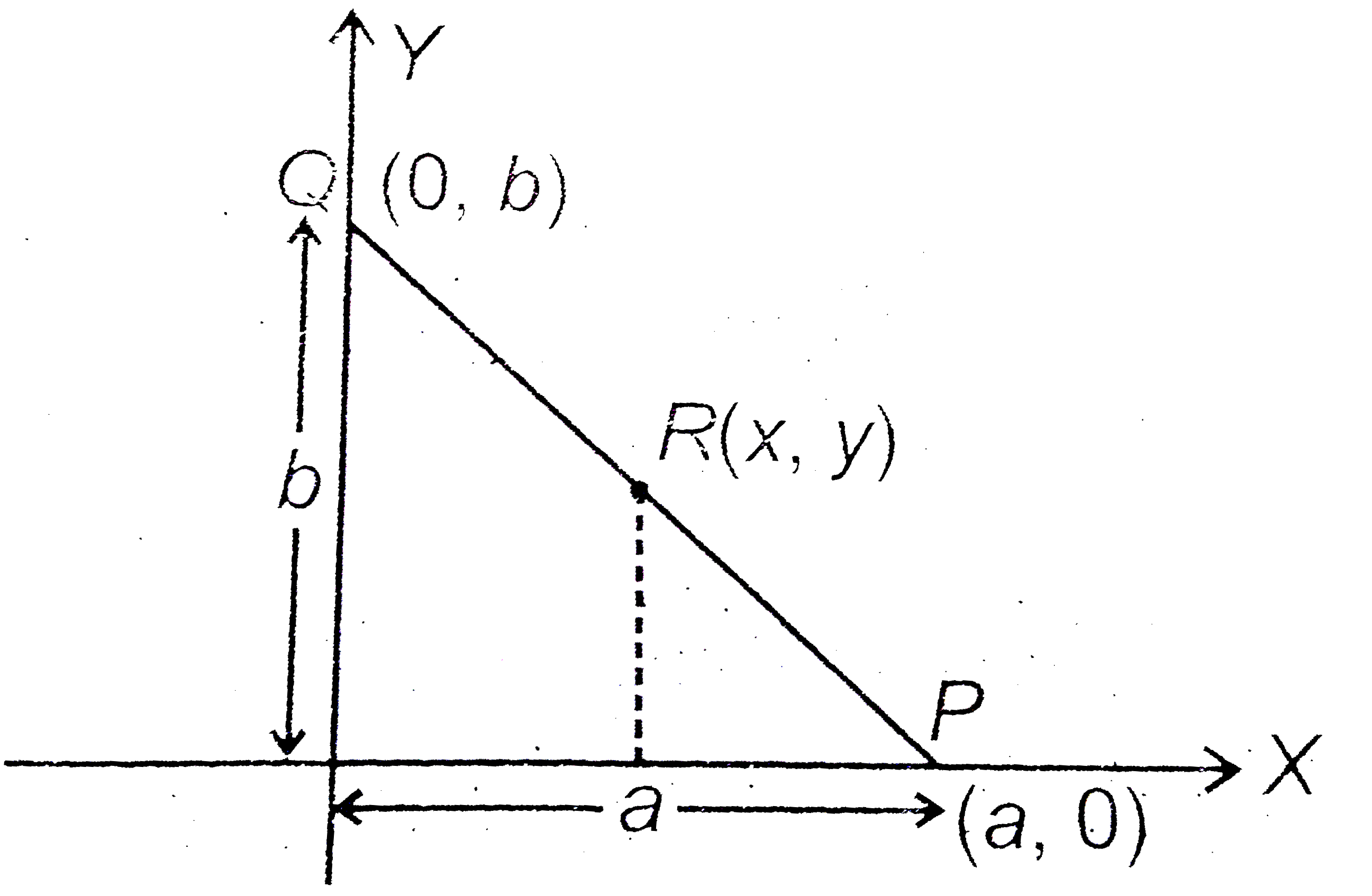
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBook:AAKASH INSTITUTEChapter:APPLICATION OF DERIVATIVESExercise:TRY YOURSELF
Explore 39 Videos
- APPLICATION OF DERIVATIVESBook:AAKASH INSTITUTEChapter:APPLICATION OF DERIVATIVESExercise:Assignment SECTION-A (Competition Level Questions)
Explore 50 Videos
- APPLICATION OF INTEGRALS Book:AAKASH INSTITUTEChapter:APPLICATION OF INTEGRALS Exercise:Assignment Section - I Aakash Challengers Questions
Explore 2 Videos
Similar Questions
A ladder 10m long rests against a vertical wall. If the foot of the ladder is 6m away from the wall and the ladder just reaches the top of the wall, how high is the wall?
View SolutionA ladder 10 meter long is leaning against a vertical wall. If the bottom of the ladder is pulled horizontally away from the wall at the rate of 1.2 meters per seconds, find how fast the top of the ladder is sliding down the wall when the bottom is 6 meters away from the wall
View Solution
Knowledge Check
A 2 m ladder leans against a vertical wall. If the top of the ladder begins to slide down the wall at the rate 25 cm/s, then the rate (in cm/s) at which the bottom of the ladder slides away from the wall on the horizontal ground when the top of the ladder is 1 m above the ground is
A25√3B25√3C253D25A 2m ladder leans against a vertical wall. If the top of the ladder begins to slide down the wall at the rate 25cm/sec., then the rate (in cm/sec.) at which the bottom of the ladder slides away from the wall on the horizontal ground when the top of the ladder is 1m above the ground is :
A25√3B25√3C253D25A ladder 5m long rests against a vertical wall. If its top slides down at the rate of 10cm/sec, then, when the foot of the ladder is 4m away from the wall, the angle between the floor and the ladder is decreasing at the rate of
Aπ4radians/sec.B4πradians/sec.C(0.025)radians/sec.Dπ6radians/sec.
A ladder 5 m long leans against a vertical wall. The bottom of the ladder is 3m from the wall. If the bottom of the ladder is pulled 1 m farther from the wall, how much does the top of the ladder slide down the wall
View SolutionA 13-m long ladder is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 m/s. How fast is its height on the wall decreasing when the foot of the ladder is 5m aways from the wall ?
View SolutionA ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
View SolutionA ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall ?
View SolutionA ladder 5 m in length is resting against vertical wall. The bottom of the ladder is pulled along the ground away from the wall at the rate of 1.5m/sec. The length of the highest point of the ladder when the foot of the ladder 4.0 m away from the wall decreases at the rate of
View Solution

