Let A={X,A,M,A,X,Y}, B={M,A,X,I,U,M} then find A∩B?
A∩B={X,A,M}
Topper's Solved these Questions
- SETS BOOK - AAKASH INSTITUTECHAPTER - SETS EXERCISE - SECTION-A(Objective Type Questions (One option is correct))
41 Videos
- SETS BOOK - AAKASH INSTITUTECHAPTER - SETS EXERCISE - SECTION-B(Objective Type Question(One option is correct))
13 Videos
- SETS BOOK - AAKASH INSTITUTECHAPTER - SETS EXERCISE - EXAMPLE
24 Videos
- SEQUENCES AND SERIES BOOK - AAKASH INSTITUTECHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - J) Aakash Challengers
12 Videos
- STATISTICSBOOK - AAKASH INSTITUTECHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason
15 Videos
Similar Questions
(i) If A={x:x2−2x+1=0}andB={x:x3−x2−2x=0}, then find A∪BandA∩B
(ii) If A={1,2,3,4},B={2,4,6,8}andU={1,2,3,....,9}, then verify that :
(A∪B)'=A'∩B'
(iii) If A={1,2,3},B={2,3,4}andU={1,2,3,4,5}, then find A'∩B'.
View Solution(i) Let A={1,2,3,4,5} and B={1,3,7,9,12} then A∩B={1,3} (ii) Let A={red, blue, green}, B={orange, yellow, red} then A∩B={red} (iii) Let X={a,e,i,o,u} and Y={a,e,i,o,u,k) then X∩Y={a,e,i,o,u}
View Solution
Knowledge Check
If A= { a,b,c} and X= {x,Y,Z} then A∩X=_____.
AABXCϕDμIf A = {a,b,c} and X = {a,b,c} , then A∩X = ________.
AABA'CϕDμ
Let A=(a,e,i,o,u},B={a,d,e,o,v}andC{e,o,t,m}.
Using Venn diagrams, verify the following :
(i) A∪(B∩C)=(A∪B)∩(A∪C)
(ii) A∩(B∪C)=(A∩B)∪(A∩C).
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
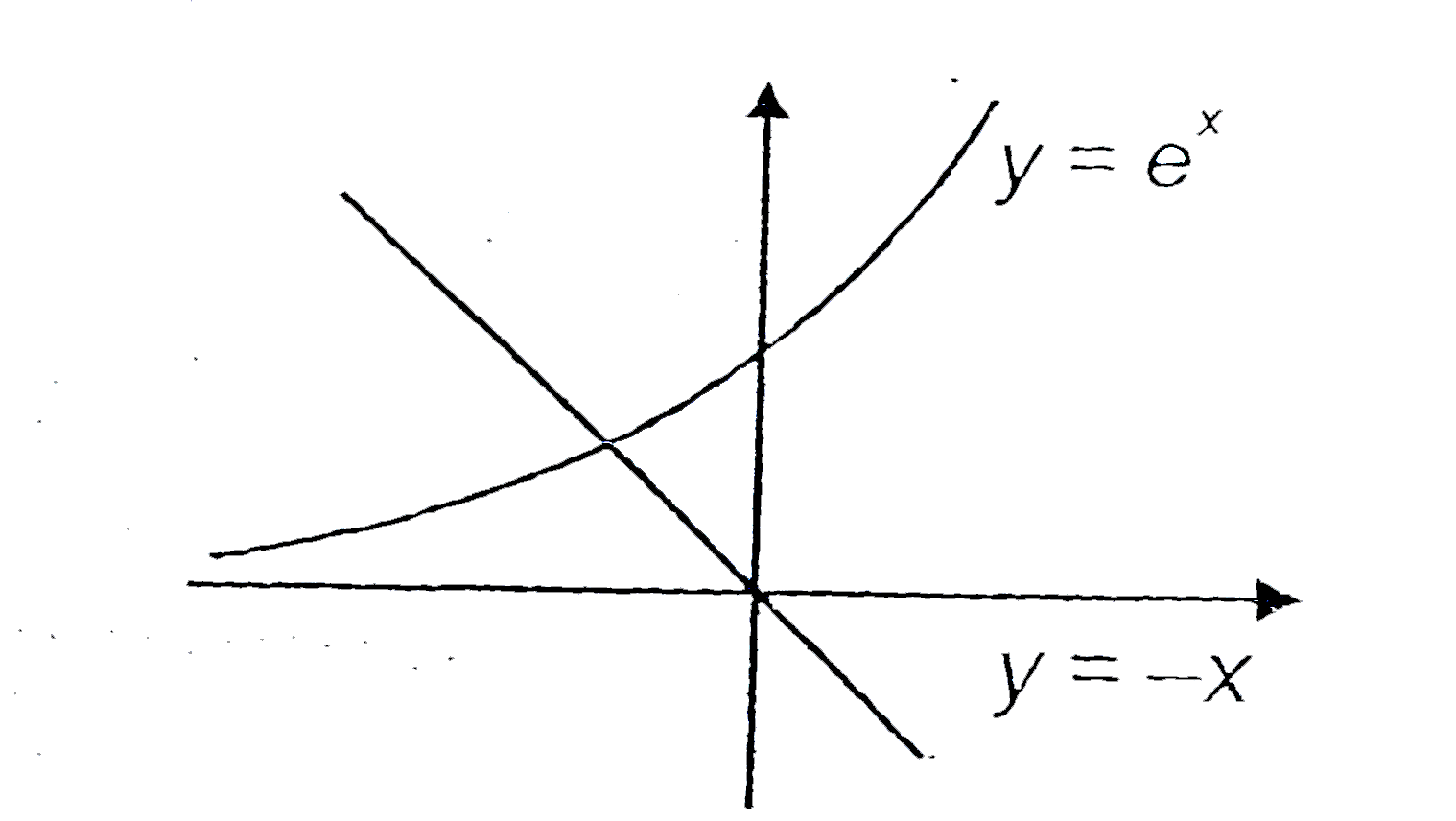
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
Then domain of A∩B is
View SolutionLet A={x:x=6n,n∈N}andB={x:x=9n,n∈N}, find A∩B.
View SolutionIf A={x:x∈R,x<5}andB={x:x∈R,x>4}, find A∩B.
View SolutionLet A = Set of all rational numbers and B={x:x2−4x+2=0}. Then find A-B,B -A and A∩ B.
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
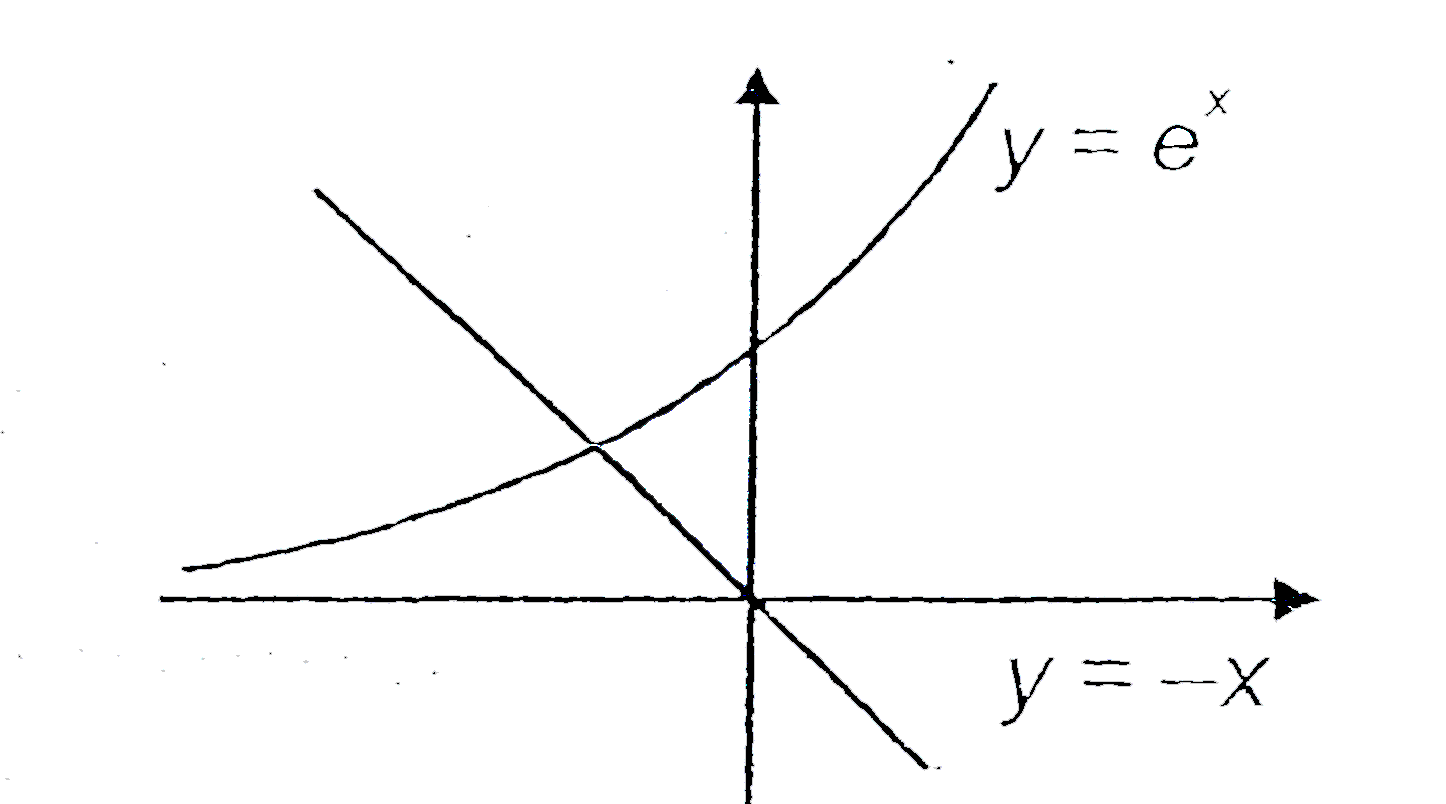
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View Solution
