STATEMENT-1: Let be rigtht angle with vertices if D is the point on AB such that the segment CD bisects angle C then the length of CD is
STATEMENT-2: The number of points on the straight line which joins to whose co-ordinates are positve interger is 3.
STATEMENT-3: If then the lines are concurrent.
F T F
T F T
T T F
F F T .
The correct Answer is:3
Step by step video, text & image solution for STATEMENT-1: Let DeltaABC be rigtht angle with vertices A(0,2),B(1,0)and C(0,0) if D is the point on AB such that the segment CD bisects angle C then the length of CD is (2sqrt2)/(3). STATEMENT-2: The number of points on the straight line which joins (-4,11) to (16,-1) whose co-ordinates are positve interger is 3. STATEMENT-3: If k=2 then the lines L_(1):2x+y-3=0,L_(2):5x+ky-3=0and L_(3):3x-y-2=0 are concurrent. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINESBook:AAKASH INSTITUTEChapter:STRAIGHT LINESExercise:SECTION-I (SUBJECTIVE TYPE QUESTIONS)
Explore 5 Videos
- STRAIGHT LINESBook:AAKASH INSTITUTEChapter:STRAIGHT LINESExercise:SECTION-J (AAKASH CHALLENGERS QUESTIONS)
Explore 5 Videos
- STRAIGHT LINESBook:AAKASH INSTITUTEChapter:STRAIGHT LINESExercise:SECTION-G (INTEGER ANSWER TYPE QUESTIONS)
Explore 4 Videos
- STATISTICSBook:AAKASH INSTITUTEChapter:STATISTICSExercise:Section-C Assertion-Reason
Explore 15 Videos
- THREE DIMENSIONAL GEOMETRY Book:AAKASH INSTITUTEChapter:THREE DIMENSIONAL GEOMETRY Exercise:ASSIGNMENT SECTION - J
Explore 10 Videos
Similar Questions
Knowledge Check
The three lines l1=4x−3y+2=0,l2=3x+4y−4=0 and l3=x−7y+6=0
Aform a rt. angled isosceles triangleBform a rt. Angled triangleCare concurrentDNoneThe lines 2x+y−1=0, ax+3y−3=0 and 3x+2y−2=0 are concurrent for -
AAll aBa= 4 onlyC1≤a≤3Da<0 onlyIf the lines 3x+4y+1=0, 5x+λy+3=0 and 2x+y-1=0 are concurrent, then λ is equal to
A−8B8C4D−4
If the straight lines 3x+4y+2=0,2x−y+3=0 and 2x+ay−6=0 are concurrent, then a=
View SolutionConsider the lines given by
L1:x+3y−5=0
L2:3x−ky−1=0
L3:5x+2y−12=0
Match the following lists.
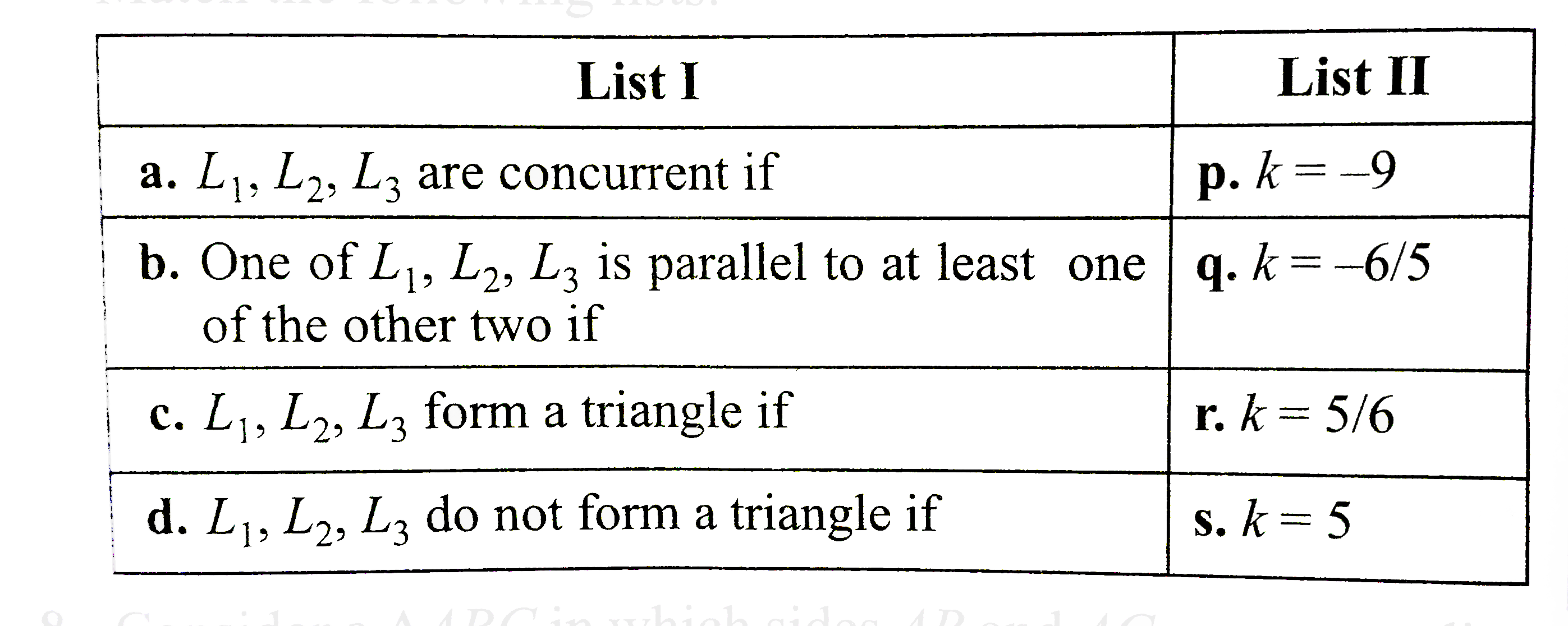
View SolutionShow that the straight lines L1=(b+c)x+ay+1=0, L2=(c+a)x+by+1=0 nd L3=(a+b)x+cy+1=0 are concurrent.
View SolutionShow that the straight lines :
x−y−1=0, 4x+3y=25 and 2x−3y+1=0 are concurrent.
View SolutionConsider the lines give by L1:x+3y−5=0,L2:3x−ky−1=0,L3:5x+2y−12=0

View Solution