(i) Find the direction in which a straight line must be drawn torough the points (1,2) so that its point of intersection with the line $x + y = 4$ may be the a distance $\sqrt{\frac{2}{3}}$ from this point.
(ii) A straight line through $P (- 15, - 10)$ meets the straight lies $x - y - 1 = 0, x + 2 y = 5 and x + 3 y = 7$ respectively at A,B and C, if $\frac{12}{P A} + \frac{40}{P B} = \frac{52}{P C},$ then prove that the straight line passes through origin.

Video Solution

Text Solution

Verified by Experts

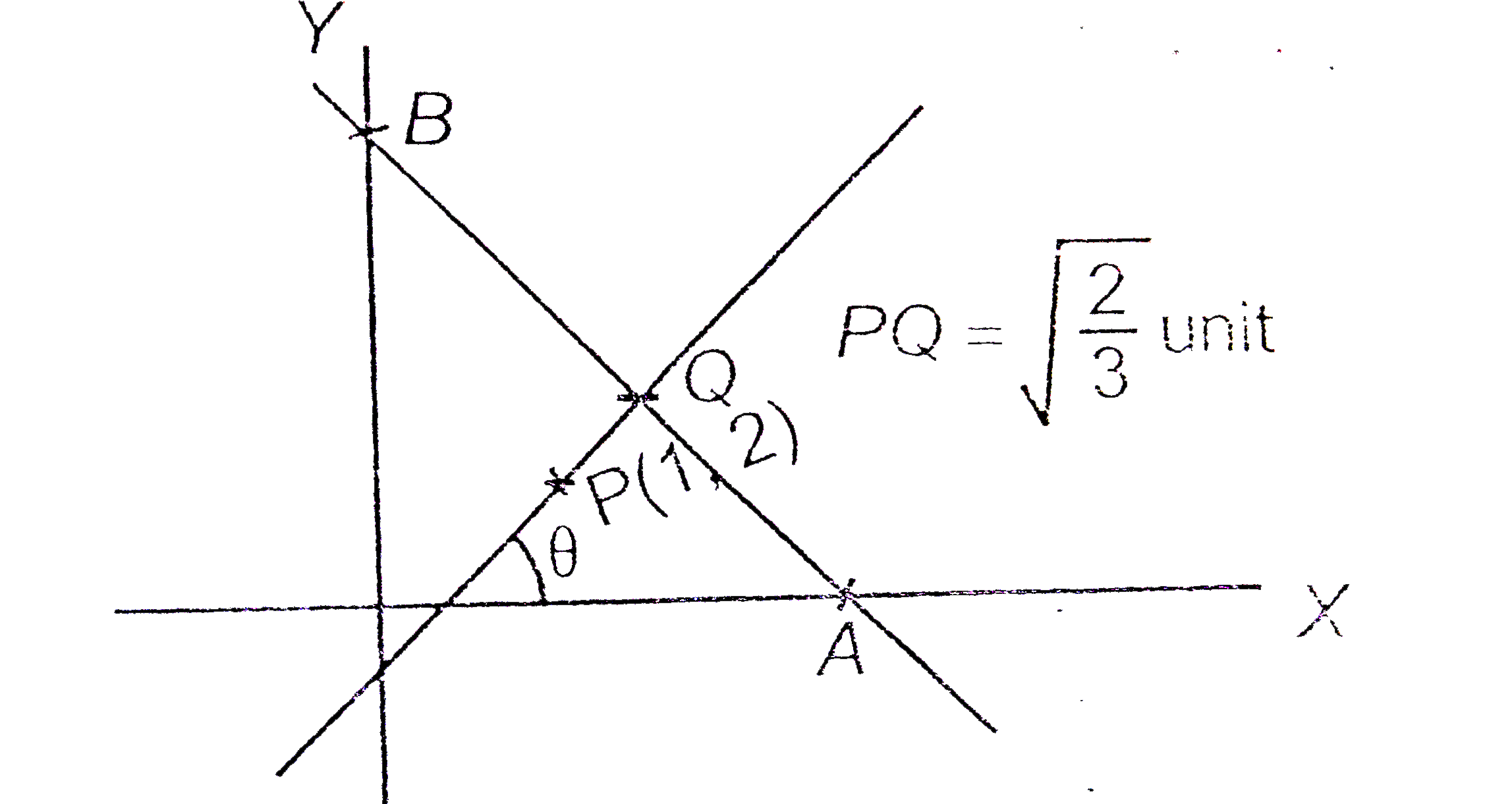
(i) Let the straight line through $P (1, 2)$ cut the given straight line $x + y = 4$ at Q and the straight line is inclined at an angle $θ$ with positive direction of x-axis. Then its equation is $\frac{x - 1}{cos θ} = \frac{y - 2}{sin θ} = r, P Q = r .$
The coordinates of the point Q are $(1 + r cos θ, 2 + r sin θ)$
Which lies on $x + y = 4$
$\Rightarrow \sqrt{\frac{2}{3}} (cos θ + sin θ) = 1, r = \sqrt{\frac{2}{3}},$ given
$\Rightarrow cos θ + sin θ = \sqrt{\frac{3}{2}}$
$\Rightarrow \frac{1}{\sqrt{2}} cos θ + \frac{1}{\sqrt{2}} sin θ = \frac{1}{\sqrt{2}} \sqrt{\frac{3}{2}} = \frac{\sqrt{3}}{2}$
$\Rightarrow cos (θ - \frac{π}{4}) = cos \frac{π}{6}$
$\Rightarrow θ - \frac{π}{4} = \frac{π}{6} or - \frac{π}{6}$
$\Rightarrow θ = \frac{π}{4} + \frac{π}{6} or \frac{π}{4} - \frac{π}{6}$
$\Rightarrow θ = \frac{5 π}{12} or = \frac{π}{12}$

(ii) Let the equation of straight line passing throug $P (- 15, - 10)$ be $\frac{x + 15}{cos θ} = \frac{y + 10}{sin θ}$
which cuts the given straight lines
$x - y - 1 = 0, x + 2 y = 5 and x + 3 y = 7$ at A, B

and C respectively.
Any point on this line may be takes as
$(- 15 + r cos θ, - 10 + r sin θ)$
For the coordinates of the point $A, (- 15 r cos θ, - 10 + r sin θ)$ lies on $x - y - 1 = 0$
$\Rightarrow - 15 + r cos θ + 10 - r sin θ - 1 = 0$
$\Rightarrow r (cos θ - sin θ) = 6$
$\Rightarrow \frac{6}{P A} = cos θ - sin θ$
Also for $B, l 15 + r cos θ - 20 + 2 r sin θ = 5$
$\Rightarrow r (cos θ + 2 sin θ) = 40$
$\Rightarrow \frac{40}{P B = cos θ 2 sin θ}$
and for the point $C, 15 + r cos θ - 30 + 3 r sin θ = 7$
$\Rightarrow r (cos θ + 2 sin θ) = 52$
$\Rightarrow cos θ + 3 sin θ = \frac{52}{P C}$
Now from the given condition,
$\frac{12}{P A} + \frac{40}{P B} = \frac{52}{P C}$
$\Rightarrow 2 (cos θ - sin θ) + cos θ + 2 sin θ = cos θ + 3 sin θ$
$\Rightarrow 2 cos θ = 3 sin θ \Rightarrow \frac{cos θ}{3} = \frac{sin θ}{2}$
Hence the required equation of the straight line is
$\frac{x + 15}{3} = \frac{y + 10}{2}$
$\Rightarrow 2 x + 30 = 3 y + 30$
$\Rightarrow 2 x - 3 y = 0$
which passes through origin.

Updated on:21/07/2023

The direction in which a straight line must be drawn through the point (1,2) so that its point of intersection with the $x + y = 4$ may be at a distance $\frac{\sqrt{6}}{3}$ from theis point is
A $30^{\circ}, 60^{\circ}$
B $15^{2}, 75^{\circ}$
C $∣ ∣$ to x-axis
D|| to y-axis
The straight line $2 x + 3 y = 12$ passes through :
A1 st, 2nd and 3rd quadrant
B1st , 2nd and 4th quadrant
C2 nd, 3rd and 4 th quadrant
D1 st, 3rd and 4th quadrant