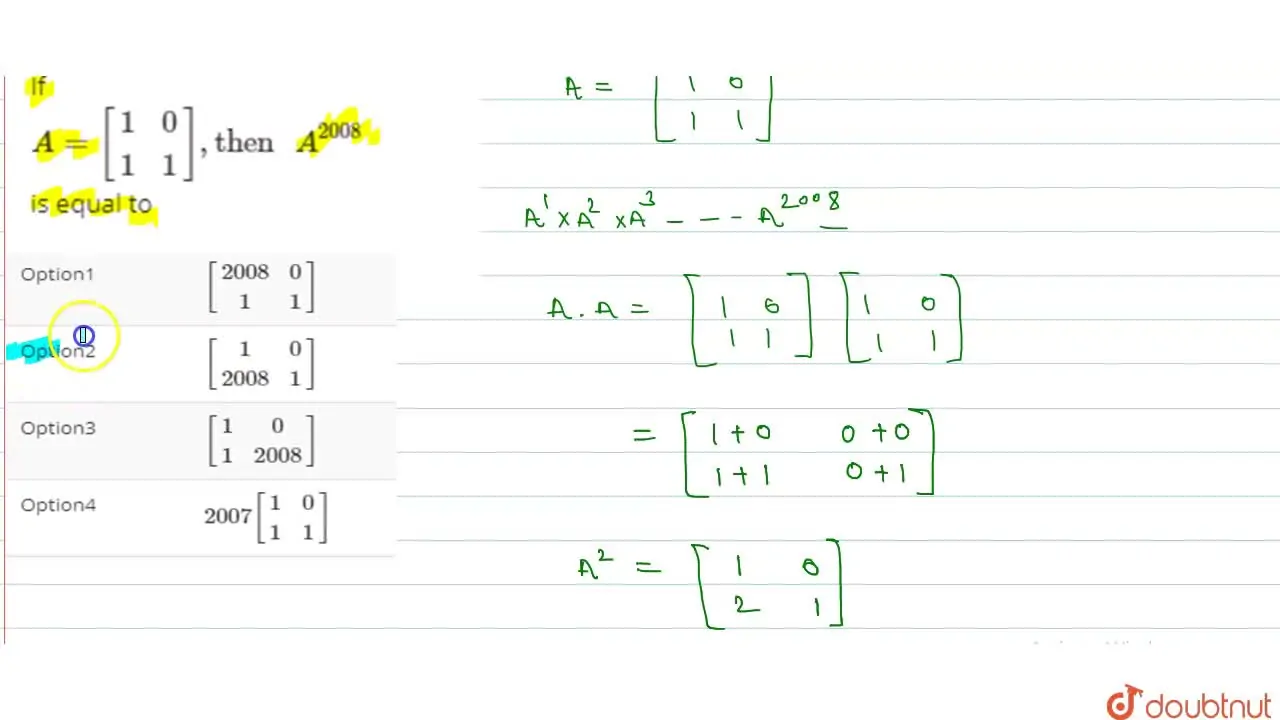If A=[1011],then A2008 is equal to
A
[2008011]
B
[1020081]
C
[1012008]
D
2007[1011]
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video, text & image solution for If A={:[(1,0),(1,1)]:},"then "A^(2008) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Assignment (Section - B) Objective Type Questions (One option is correct)13videos
MATRICES
- BOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Assignment (Section - C) Objective Type Questions (More than one options are correct)7videos
MATRICES
- BOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Try yourself12videos
MATRICES
- BOOK - AAKASH INSTITUTECHAPTER - MATHEMATICAL REASONINGEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)15videos
MATHEMATICAL REASONING
- BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section-J (Aakash Challengers Questions)7videos
PERMUTATIONS AND COMBINATIONS
Similar Questions
If A = [1011] then An is equal to
View Solution10.04 is equal to :
View SolutionIfA=⎡⎢⎣100010ab−1⎤⎥⎦, then A2 is equal to
View SolutionIf A=[101/21], A400 is equal to
View SolutionIf A=[0110] then A2 is equal to
View SolutionIf A=(1−112)and I=(1001) then 3A−1 is equal to :
View SolutionA=[0110] ,then A2 is equal to
View SolutionIf A=⎡⎢⎣100010ab−1⎤⎥⎦, then A2 is equal to
View SolutionIf A=[10121] , then A100 is equal to
View SolutionIfA=[0110], then A2 is equal to
View Solution