How many four-digit numbers are there whose decimal notation contains not more than two distinct digits?
Video Solution
Text Solution
We have to form four-digit numbers whose decimal notation contains one or two different digits. Clearly the number of four-digit numbers with one digit such as 1111, 2222)=9 etc.
Let us consider two different digits
Here two cases arise.
Case I :
Out of two digits, one digits is 0. We can select other non-zero digit in 9C1 =0 ways. Let us consider the  digits 1,0 . Then the four digits numbers are 1110, 1100, 1000 and their arrangements . When thousand place is 1, the remaining places can be arranged in (3!2!+3!2!+1)=7 ways
digits 1,0 . Then the four digits numbers are 1110, 1100, 1000 and their arrangements . When thousand place is 1, the remaining places can be arranged in (3!2!+3!2!+1)=7 ways
∴ The number of required number =7×9=63
Case II
Two digits are non-two different digits. We can select two different non-zero digit out of 9 non zero digits in 9C2 = 36 ways .
Let us proceed with 1,2
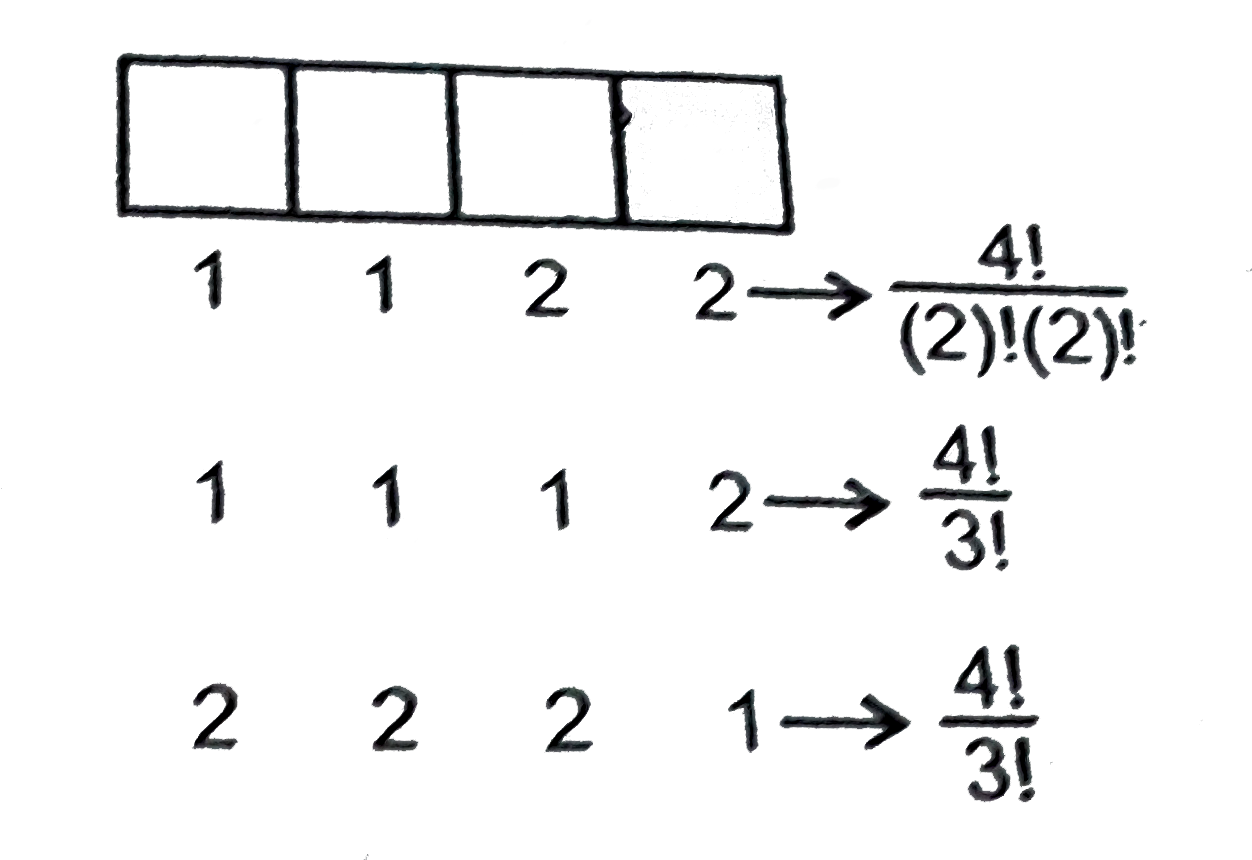
Then possible combinations for four digitts are 1,1,2,2,1,1,1,2 and 2,2,2,1 and their corresponding arrangements are 4!(2)!(2)!,4!3!and4!3! respectively .
Hence the number of four digits numbers under given condition
=9C2(6+4+4)=36×14=504
∴ Total number of four-digit numbers whose decimal notation contains not more than two distinct digits.
=9+63+504=576
|
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Try Yourself
65 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section A Objective type questions (One option is correct )
51 Videos
- MATRICESBOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Assignment (Section - J) Aakash Challengers Questions
3 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTECHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)
12 Videos
Similar Questions
Knowledge Check
How many 4-digit numbers are there with no digit repeated?
A=9⋅9⋅8⋅7B=10⋅9⋅8⋅7C=9⋅8⋅7DNone of theseHow many two -digit numbers are divisible by 3?
A25B30C32D36
How many 3-digit numbers are there with no digit repeated?
View SolutionHow many 3-digit numbers are there with no digit repeated?
View SolutionHow many two-digit numbers are divisible by 9?
View SolutionHow many two-digit numbers are divisible by 5?
View SolutionHow many three digit numbers are there with no digit repeated?
View SolutionHow many three digit numbers are there, with no digit repeated.
View Solution
