There are p intermediate stations on a railway line from one terminus to another . In how many ways a train can stop at 3 of these intermediate stations if no two of those stopping stations are to be consecutive ?

Video Solution

Text Solution

Verified by Experts

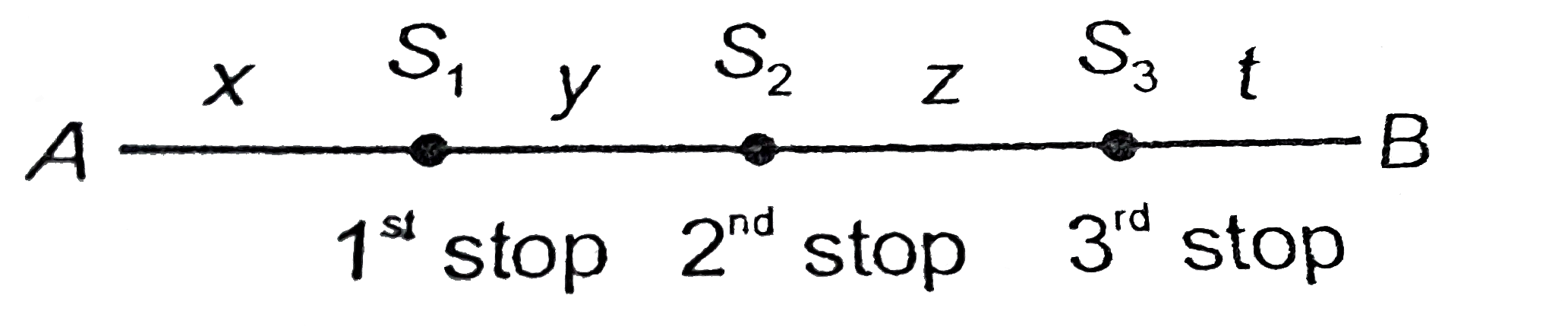
Let x, y, z and t be the numbers of stations before first stoppage, between first and second stoppage , between second and third stoppages , after third stoppage respevtively , then
$x \geq 0, y \geq 1, z \geq 1, t \geq 0 and x + y + z + t = p - 3$ .
Let $y = 1 + y_{1}, and z = 1 + z_{1}$ , so that $y_{1} \geq 0, z_{1} \geq 0 and x + y_{1} + z_{1} + t = p - 5 .$ The no. of non-negative integral solution of $x + y_{1} + z_{1} + t = p - 5$ is
$=^{p - 5 + 4 - 1} C_{4 - 1} =^{p - 2} C_{3} = \frac{(p - 2) (p - 3) (p - 4)}{6}$

Updated on:21/07/2023

Between two junction stations A and B there are 12 intermediate stations. The total numbre of ways in which a train can be made to stop at 4 of these stations so that no two of these halting stations are consecutive, is
A $^{9} C_{5}$
B $^{9} C_{4}$
C $^{10} C_{4}$
D $^{10} C_{5}$
Between two junction stations A and B there are 12 intermediate stations. The number of ways in which a train can be made to stop at 4 of these stations so that no two of these halting stations are consecutive, is
A $^{8} C_{4}$
B $^{9} C_{4}$
C $^{12} C_{4} - 4$
Dnone of these
Between two junction stations A and B, there are 12 intermediate stations. The number of ways in which a train can be made to stop at 4 of these stations so that no two of these halting stations are consecutive, is
A $^{8} C_{4}$
B $^{9} C_{4}$
C $^{12} C_{4} - 4$
Dnone of these