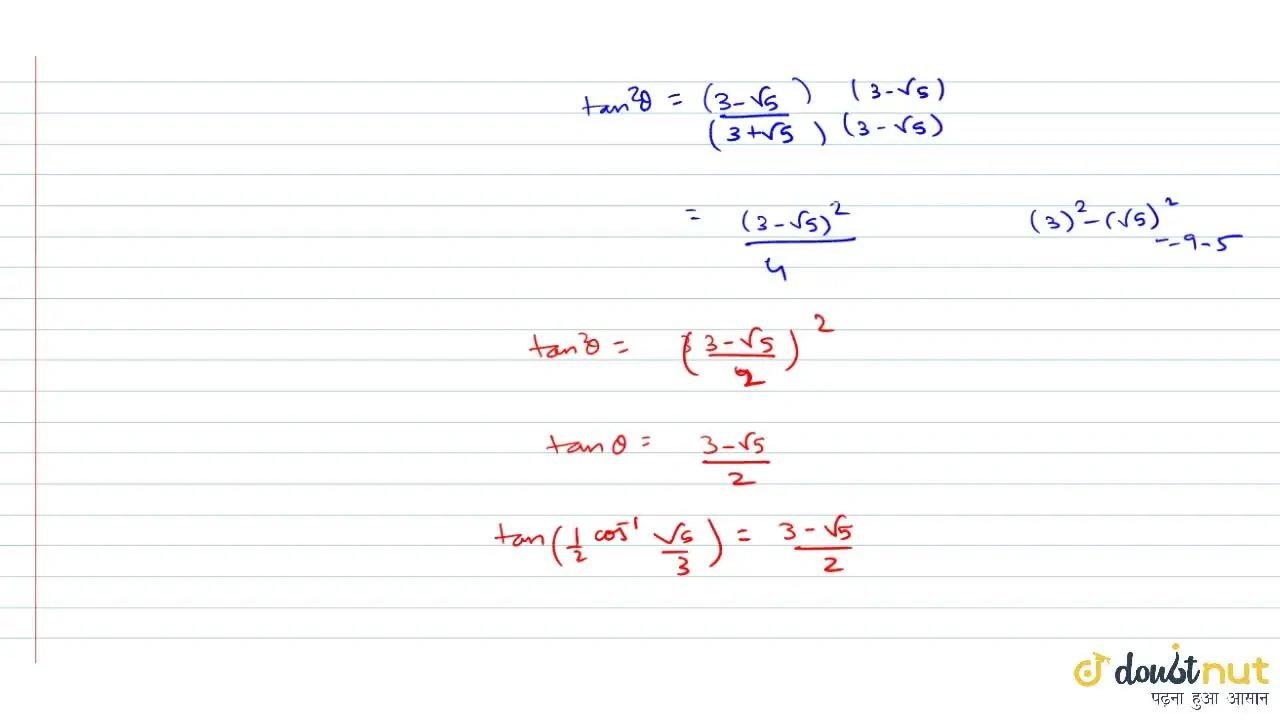tan(12cos−1 √53)
A
3−√52
B
3+√52
C
5−√32
D
5+√32
Video Solution
Text Solution
The correct Answer is:A
Let cos−1√53=θ. Then, cosθ=√53.
tan12(cos−1√53)=tan12θ=sin(θ2)cos(θ2).
=√1−cosθ1+cosθ=⎧⎪⎨⎪⎩1−√531+√53⎫⎪⎬⎪⎭1/2
(3−√53+√5)1/2={3−√53+√5×3−√53−√5}1/2=3−√52.
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - INVERSE TRIGNOMETRIC FUNCTIONS EXERCISE - Exercise 4D6videos
INVERSE TRIGNOMETRIC FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - INTEGRATION USING PARTIAL FRACTIONSEXERCISE - Objective Questions Ii37videos
INTEGRATION USING PARTIAL FRACTIONS
- BOOK - RS AGGARWALCHAPTER - LINEAR DIFFERENTIAL EQUATIONS EXERCISE - Objective Questions27videos
LINEAR DIFFERENTIAL EQUATIONS
Similar Questions
Evaluate:
i) sin{π3−sin−1(−12)}
ii) sin(12cos−145)
iii) sin(cot−1x)
iv) tan12(cos−1√53)View SolutionFind the value of tan(12cos−1.√53)
View SolutionFind the value of tan(12cos−1.√53)
View SolutionFind the value of tan(12cos−1(√53))
View SolutionThe value of tan[12cos−1(√53)] is
View SolutionEvaluate: tan{12cos−1(√53)}
View SolutionThe value of tan[12cos−1(√53)] is :
View SolutionThe value of tan(12cos−1'2√5) is
View SolutionThe value of the expression tan(12cos−12√5) is
View SolutionThe value of tan[12cos−1.√53] is
View Solution