Which species of protist are known as the whirling whips because of the spins produced by two flagella beating in opposing grooves along their hard surfaced bodies?
Golden brown algae
Chrysophytes
Diatoms
Dinoflagellates
The correct Answer is:D
Step by step video, text & image solution for Which species of protist are known as the whirling whips because of the spins produced by two flagella beating in opposing grooves along their hard surfaced bodies? by Biology experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROTISTABOOK - ARIHANT NEETCHAPTER - PROTISTAEXERCISE - CHAPTER EXERCISES ((B) MEDICAL ENTRANCES SPECIAL FORMAT QUESTIONS (Statement based questions))
9 Videos
- PROTISTABOOK - ARIHANT NEETCHAPTER - PROTISTAEXERCISE - CHAPTER EXERCISES ((B) MEDICAL ENTRANCES SPECIAL FORMAT QUESTIONS (Match the column))
2 Videos
- PROTISTABOOK - ARIHANT NEETCHAPTER - PROTISTAEXERCISE - CHECK POINT 5.4
20 Videos
- PLANTAEBOOK - ARIHANT NEETCHAPTER - PLANTAEEXERCISE - Chapter Exercises (C Medical entrances gallery)
80 Videos
- REPRODUCTION IN ORGANISMS BOOK - ARIHANT NEETCHAPTER - REPRODUCTION IN ORGANISMS EXERCISE - CHAPTER EXERCISES (C) Medical entrances gallery (Collection f the following statement is not correct)
14 Videos
Similar Questions
Two independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Distance of a point from O, at which the sixth order minimum is formed, will be
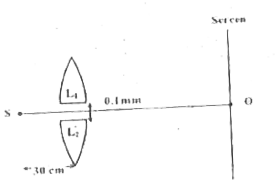
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q0.25 mm
View Solution
Knowledge Check
Which species of protists are known as the whirlin whips?
ADiatomsBChrysophytesCDinoflagellatesDgolden-brown algaeWhirling Whips are protists which possess two flagella that beat
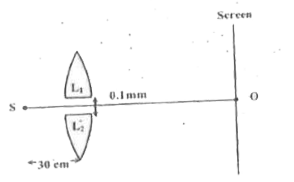
ASlighty towards one side so as to cause rotation of the organism while moving forwordBForword, backword and sideways depending upon the reqirementCAt right angles to each other due to being present in different groovesDAlong with numerous cilia.Two independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Phase difference between the light waves 0.1 mm from along the screen, where intensity is half the maximum value, is
 A) tt/2Bk/3Ctt/4Dir/6
A) tt/2Bk/3Ctt/4Dir/6
Two independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
QDistance between the images Si and S2 will be
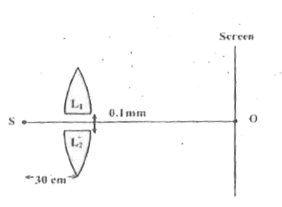
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Fringe width is nearly
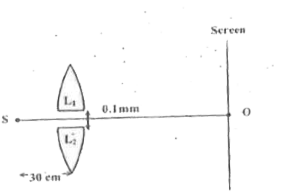
View SolutionComprehension:
Read the following passage and answer the questions given after it.
There are three main groups of oils: animal, vegetable and mineral. Great quantities of animal oil come from whales, those enormous creatures of the sea which are the largest remaining animals in the world. To protect the whale from the cold of the Arctic seas, nature has provided it with a thick covering of fat called blubber. When the whale is killed, the blubber is stripped off and boiled down. It produces a great quantity of oil which can be made into food for human consumption. A few other creatures yield oil, but none so much as the whale. The livers of the cod and the halibut, two kinds of fish, yield nourishing oil. Both cod liver oil and halibut liver oil are given to sick children and other invalids who need certain vitamins.
Vegetable oil has been known from antiquity. No household can get on without it, for it is used in cooking. Perfumes may be made from the oils of certain flowers. Soaps are made from vegetable and animal oils.
To the ordinary man, one kind of oil may be as important as another. But when the politician or the engineer refers to oil, he almost always means mineral oil, the oil that drives tanks, aeroplanes and warships, motor-cars and diesel locomotives, the oil that is used to lubricate all kinds of machinery. This is the oil that has changed the life of the common man. When it is refined into petrol it is used to drive the internal combustion engine. To it we owe the existence of the motorcar, which has replaced the private carriage drawn by the horse. To it we owe the possibility of flying. It has changed the methods of warfare on land and sea. This kind of oil comes out of the earth. Because it burns well, it is used as fuel and in some ways it is superior to coal in this respect. Many big ships now burn oil instead of coal. Because it burns brightly, it is used for illumination, countless homes are still illuminated with oil-burning lamps. Because it is very slippery, it is used for lubricating the machines.
Many big ships now burn oil instead of coal because it:
View SolutionComprehension:
Read the following passage and answer the questions given after it.
There are three main groups of oils: animal, vegetable and mineral. Great quantities of animal oil come from whales, those enormous creatures of the sea which are the largest remaining animals in the world. To protect the whale from the cold of the Arctic seas, nature has provided it with a thick covering of fat called blubber. When the whale is killed, the blubber is stripped off and boiled down. It produces a great quantity of oil which can be made into food for human consumption. A few other creatures yield oil, but none so much as the whale. The livers of the cod and the halibut, two kinds of fish, yield nourishing oil. Both cod liver oil and halibut liver oil are given to sick children and other invalids who need certain vitamins.
Vegetable oil has been known from antiquity. No household can get on without it, for it is used in cooking. Perfumes may be made from the oils of certain flowers. Soaps are made from vegetable and animal oils.
To the ordinary man, one kind of oil may be as important as another. But when the politician or the engineer refers to oil, he almost always means mineral oil, the oil that drives tanks, aeroplanes and warships, motor-cars and diesel locomotives, the oil that is used to lubricate all kinds of machinery. This is the oil that has changed the life of the common man. When it is refined into petrol it is used to drive the internal combustion engine. To it we owe the existence of the motorcar, which has replaced the private carriage drawn by the horse. To it we owe the possibility of flying. It has changed the methods of warfare on land and sea. This kind of oil comes out of the earth. Because it burns well, it is used as fuel and in some ways it is superior to coal in this respect. Many big ships now burn oil instead of coal. Because it burns brightly, it is used for illumination, countless homes are still illuminated with oil-burning lamps. Because it is very slippery, it is used for lubricating the machines.
Which of the following is NOT a use of vegetable oil?
View SolutionComprehension:
Read the following passage and answer the questions given after it.
There are three main groups of oils: animal, vegetable and mineral. Great quantities of animal oil come from whales, those enormous creatures of the sea which are the largest remaining animals in the world. To protect the whale from the cold of the Arctic seas, nature has provided it with a thick covering of fat called blubber. When the whale is killed, the blubber is stripped off and boiled down. It produces a great quantity of oil which can be made into food for human consumption. A few other creatures yield oil, but none so much as the whale. The livers of the cod and the halibut, two kinds of fish, yield nourishing oil. Both cod liver oil and halibut liver oil are given to sick children and other invalids who need certain vitamins.
Vegetable oil has been known from antiquity. No household can get on without it, for it is used in cooking. Perfumes may be made from the oils of certain flowers. Soaps are made from vegetable and animal oils.
To the ordinary man, one kind of oil may be as important as another. But when the politician or the engineer refers to oil, he almost always means mineral oil, the oil that drives tanks, aeroplanes and warships, motor-cars and diesel locomotives, the oil that is used to lubricate all kinds of machinery. This is the oil that has changed the life of the common man. When it is refined into petrol it is used to drive the internal combustion engine. To it we owe the existence of the motorcar, which has replaced the private carriage drawn by the horse. To it we owe the possibility of flying. It has changed the methods of warfare on land and sea. This kind of oil comes out of the earth. Because it burns well, it is used as fuel and in some ways it is superior to coal in this respect. Many big ships now burn oil instead of coal. Because it burns brightly, it is used for illumination, countless homes are still illuminated with oil-burning lamps. Because it is very slippery, it is used for lubricating the machines.
For engineers which oil is meaningful?
View Solution
