Simplify sin(cot−1(cos(tan−1x))),0<x<1.
Video Solution
Text Solution
y=sin(cot−1(cos(tan−1x)))
Let tan−1x=θ
⇒x=tanθ
∴y=sin(cot−1(cosθ))
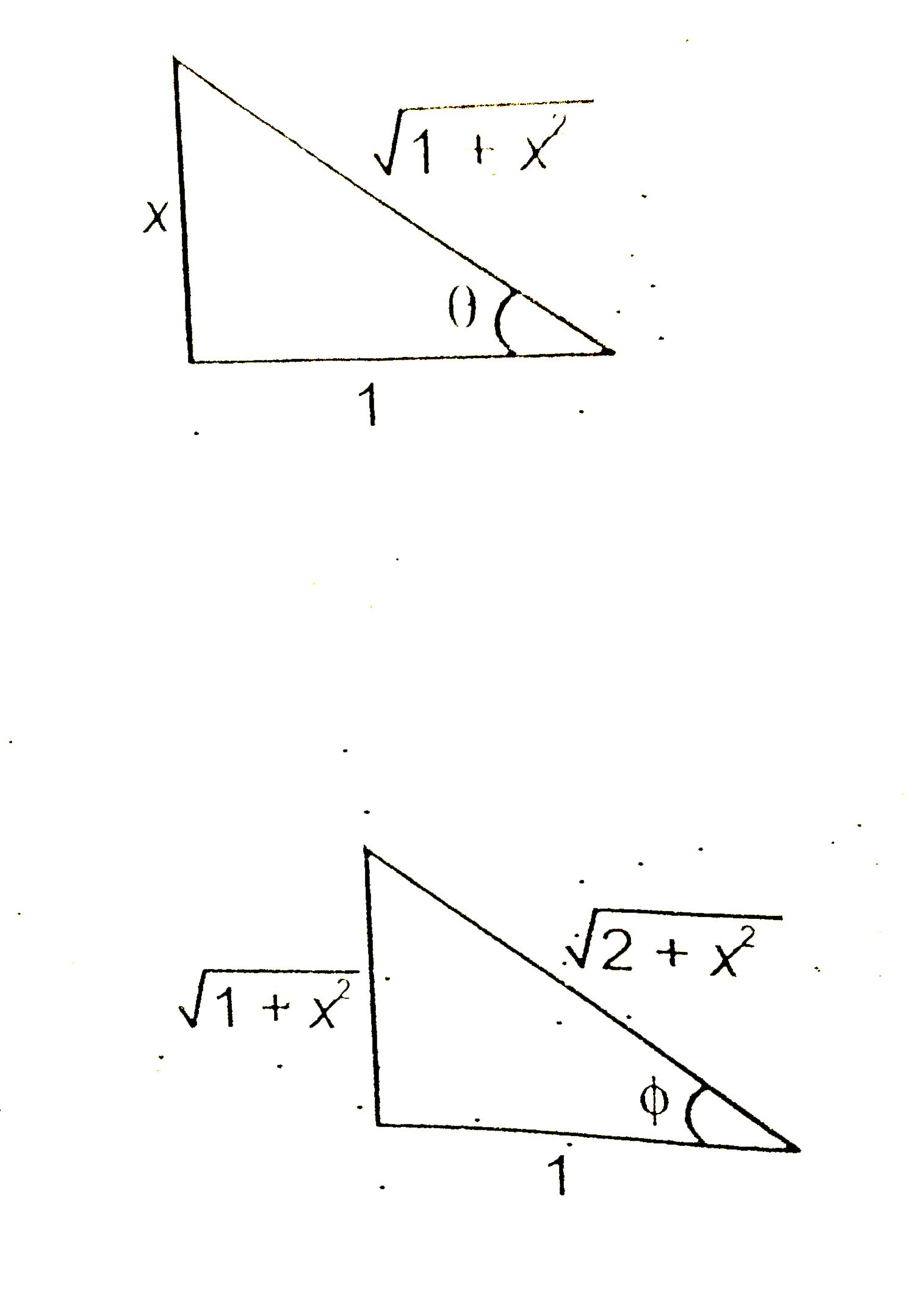
=sin(cot−1(1√1+x2)
Let cot−1(1√1+x2)=ϕ
⇒cotϕ=1√1+x2
⇒y=sinθ
=√1+x22+x2
|
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONSBook:AAKASH INSTITUTEChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:TRY YOURSELF
Explore 21 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:AAKASH INSTITUTEChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:ASSIGNMENT (SECTION - A)(OBJECTIVE TYPE QUESTIONS (ONE OPTION IS CORRECT))
Explore 45 Videos
- INTEGRALSBook:AAKASH INSTITUTEChapter:INTEGRALSExercise:Try yourself
Explore 50 Videos
- LIMITS AND DERIVATIVES Book:AAKASH INSTITUTEChapter:LIMITS AND DERIVATIVES Exercise:Section - j
Explore 3 Videos
Similar Questions
Knowledge Check
sin{cot−1[tan(cos−1x)]=
AxBπ2C1Dnone of theseThe value of x for which sin(cot−1(1+x))=cos(tan−1x) is
A1/2B1C0D−1/2The value of sin(cot−1(cos(tan−1x))) is
A√x2+2x2+1B√x2+1x2+2Cx√x2+2D1√x2+2

