Spring constant of a spring is calculated using formule , where T is time period of vertical oscillation when mass M is hung with the help of spring to rigid support. If time of oscillation for 10 oscillations is measured to be 5.0 s and mass M=0.20 kg, find possible error in spring constant K.
The correct Answer is:2.9 N/m
Step by step video, text & image solution for Spring constant of a spring is calculated using formule K=(4pi^2M)/T^2, where T is time period of vertical oscillation when mass M is hung with the help of spring to rigid support. If time of oscillation for 10 oscillations is measured to be 5.0 s and mass M=0.20 kg, find possible error in spring constant K. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- UNITS AND MEASUREMENTSBook:AAKASH INSTITUTEChapter:UNITS AND MEASUREMENTSExercise:EXERCISE
Explore 20 Videos
- UNITS AND MEASUREMENTSBook:AAKASH INSTITUTEChapter:UNITS AND MEASUREMENTSExercise:ASSIGNMENT (SECTION - A)
Explore 50 Videos
- UNITS AND MEASUREMENTSBook:AAKASH INSTITUTEChapter:UNITS AND MEASUREMENTSExercise:ASSIGNMENT SECTION I (Subjective)
Explore 18 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTEChapter:THERMODYNAMICSExercise:ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
Explore 10 Videos
- WAVE OPTICSBook:AAKASH INSTITUTEChapter:WAVE OPTICSExercise:Assignment (Section-J (Aakash Challengers question))
Explore 1 Video
Similar Questions

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
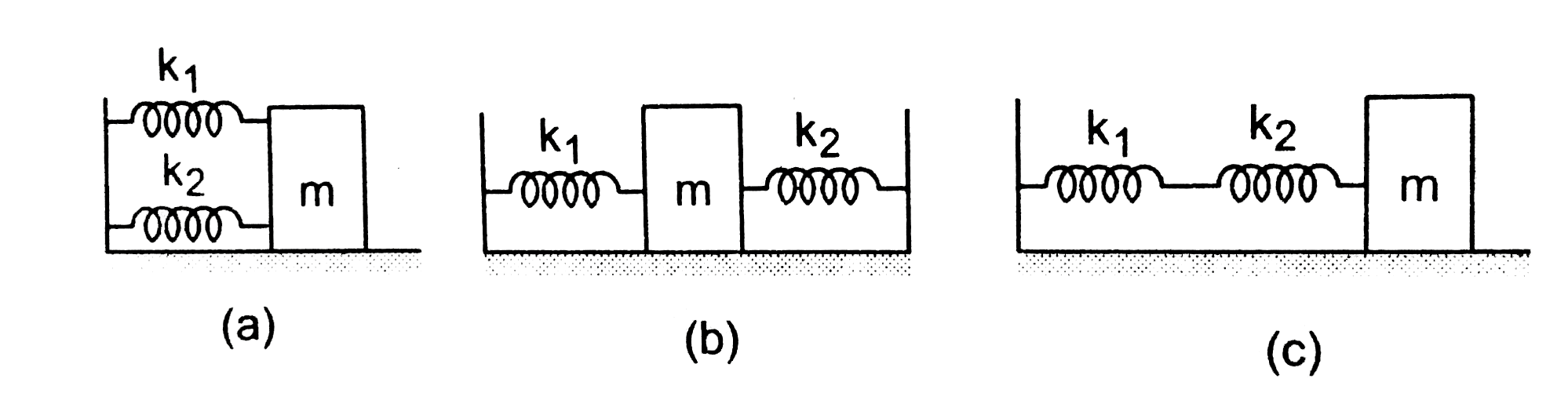
View Solution
Knowledge Check
Calculate the period of oscillations of block of mass m attached with a set of springs as shown
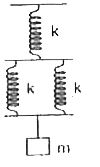 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2kThe time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is
A0.2πsB0.21πsC0.22πsD0.02πs
A spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionThe graph between period of oscillation (T) and mass attached (m) to a spring will be
View SolutionIf the period of oscillation of mass m suspended from a spring is 2 s, then the period of mass 4 m will be
View SolutionWhen a mass M is suspended from a spring, its period of oscillation is 2 second. If a mass 4 M is suspended from the same spring, then its period of oscillation will be
View SolutionThe period of oscillation of mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be
View Solution

