The kinetic energy of a particle moving along x-axis varies with the d

The potential energy U of a particle varies with distance x from a fixed origin as $U = \frac{A \sqrt{x}}{x^{2} + B}$ where A and B are dimensional constants. The dimensional formula for AB is
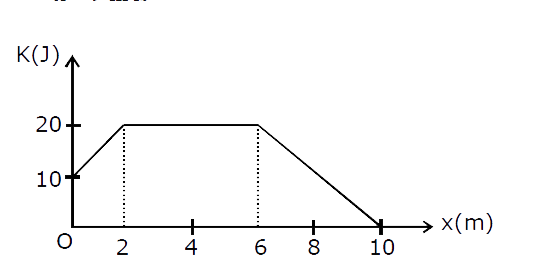
A $[M^{1} L^{7 / 2} T^{- 2}]$
B $[M^{1} L^{11 / 2} T^{- 2}]$
C $[M^{1} L^{5 / 2} T^{- 2}]$
D $M^{1} L^{9 / 2} T^{- 2}]$
The kinetic energy K of a particle moving along x - axis varies with its position (x) as shown in figure

The magnitude of force acting on particle at x = 9 mis
AZero
B5 N
C20 Ns
D7.5 N
Velocity time graphs of particles $A$ and $B$ moving along $x$ -axis are shown here. Both $A$ and $B$ start from origin:
AMaximum separation between the particles is $8 m$
BMaximum separation between the particles is $10 m$
CMaximum separation between the particles occurs at $t = 6 s$
DMaximum separation between the particles occurs at $t = 8 s$

The kinetic energy of a particle moving along x-axis varies with the distance x of the particle from origin as $K = \frac{A + x^{3}}{B x^{1 / 4} + C}$ .Write the dimensional formula for $A^{2} B$