What is the magnetic force acting on the finite wire due to the fixed infinite wire shown here?
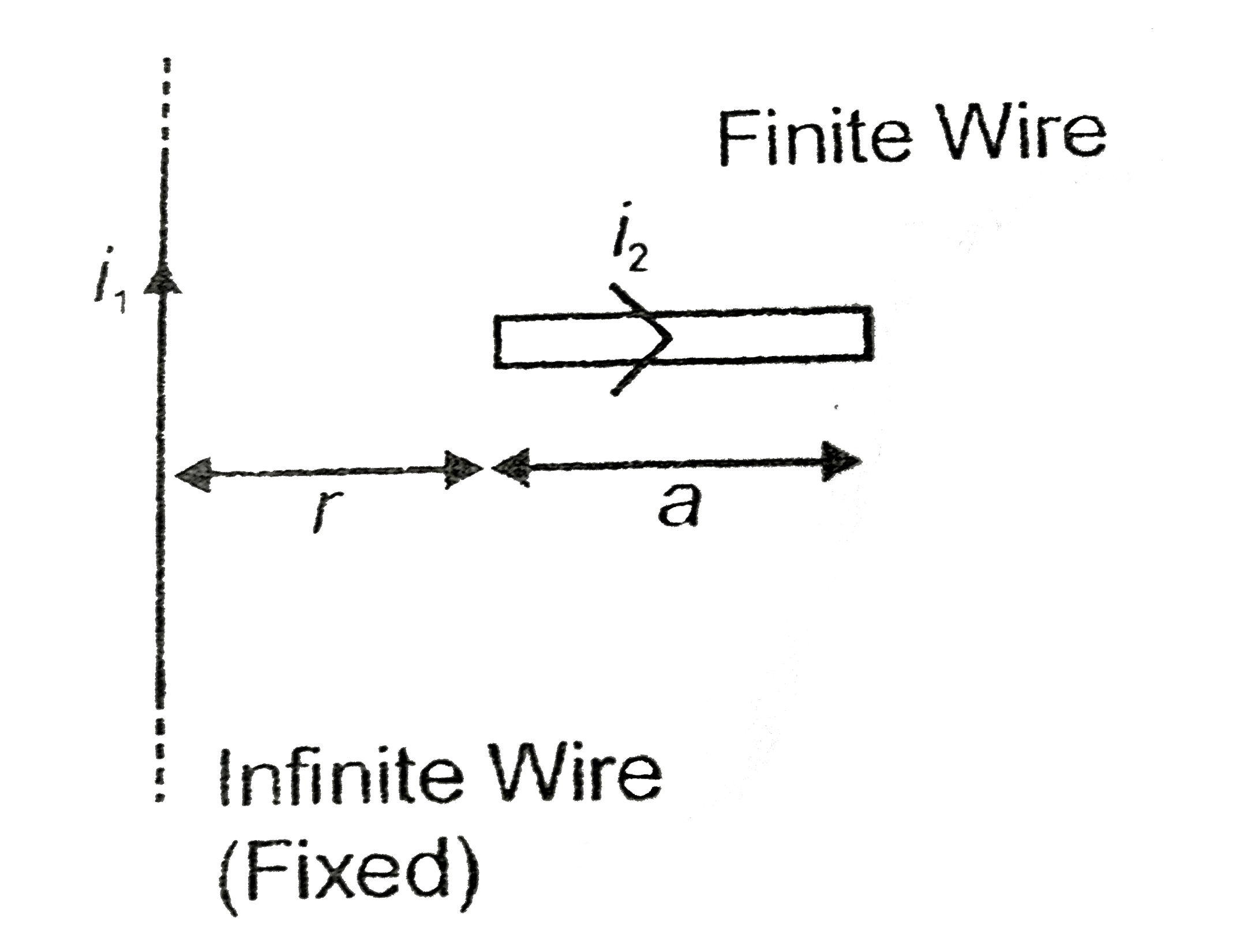
Strategy: We cannot use formula →F=i→l×→B to find the force as the magnetic field created by the fixed infinite wire is non-uniform. We have to consider an element on the finite wire, find force on it and integrate to obtain the net force.
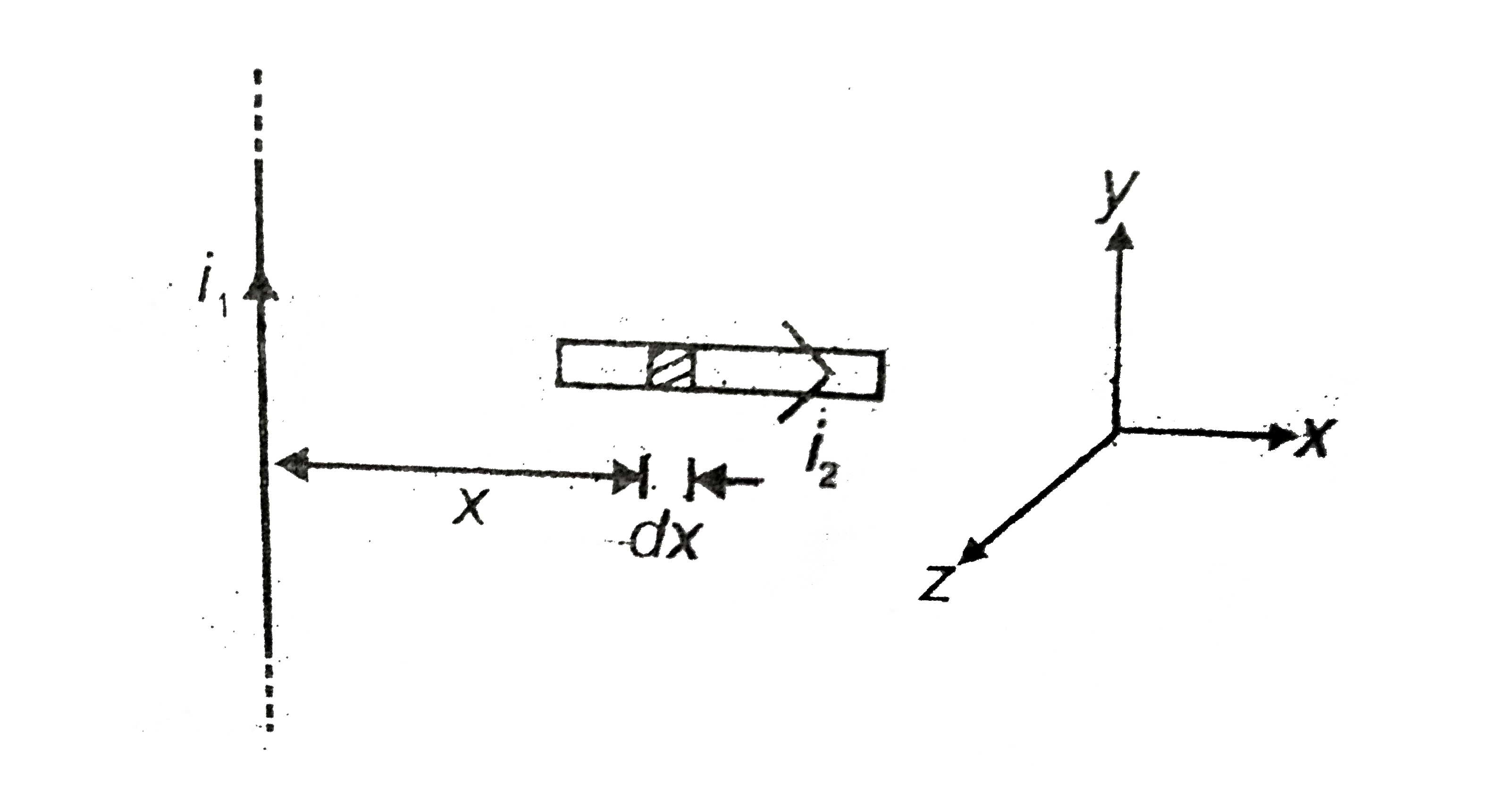
Let us consider an element of length dx on the finite wire at a distance x from the infinite wire as shown.
Force on the element,
−→dF=i→dl×→B=i2⎛⎜
⎜⎝dxˆi×μ0i1(−ˆk)2πx⎞⎟
⎟⎠=μ0i1i2dx2πxˆj
Net force on the wire,
→F=∫d→F=∫r+arμ0i1i22πxdxˆj
=μ0i1i22πx∫r+ardxxˆj
=μ0i1i22πx[lnx]r+ar
=μ0i212πxln(r+ar)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration
12 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself
27 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Knowledge Check
A semicircular ring is present in the uniform magnetic field. Magnetic field is perpendicular to loop of ring. Assertion: Force →F on each element of ring is different
Reason: Net force on ring must be perpendicular to magnetic field.AIf both the assertion and reason are true and reason is a true explantion of the assertion.BIf both the assertion and reason are true but the reason is not true the correct explantion of the assertion.CIf the assertion is true but reason falseDIf both the assertion and reason are false.Figure shows four wires placed in the same uniform magnetic field B and carrying the same current in which case force acting on the wire is minimum
A B
B C
C D
D

A conducting wire MN carrying a current I is bent into the shape as shown and placed in xy plane. A uniform magnetic field →B=−Bˆk is existing in the region. The net magnetic force experenced by the conducting wire MN isA2BIRB3BIRC4BIRD6BIR
Prove that the force acting on a current carrying wire, joining two fixed points a and b in a uniform magnetic field, is independent of the shap of the wire.
View SolutionA triangular loop (ABC) having current i2 and an infinite wire having current i1 are placed in the same plane.Find the magnetic force of interaction between the infinite wire and the loop ABC.
View SolutionA wire of length l carries a current I along the x-asis. A magnetic field exists which is given as →B=B0(→i+→j+→k) T. find the magnitude of the magnetic force acting on the wire.
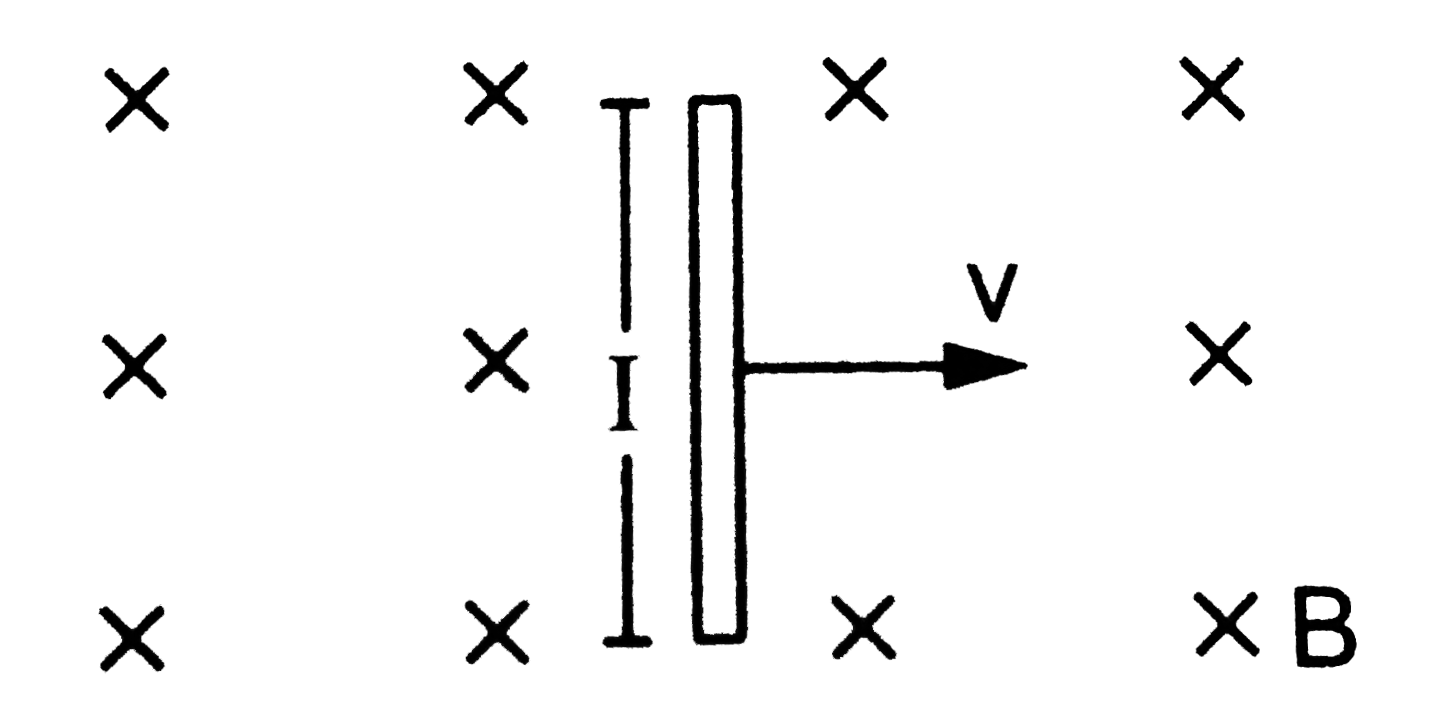
View SolutionA conducting wire of length l, lying normal to a magnetic field B, moves with a velocity v as shown in (a) Find the average magnetic fore on a free electron of the wire. Due to this magnetic force, electrons concentrate at one end resulting in an electric field inside the wire. The redistribution stops when the electric force on the free electrons balances themagnetic force. Find the electric field developed inside the wire when the redistribution field developed inside the wire when the redistribution stops. (c) what potential difference is developed between the ends of the wire?
View SolutionA: A bar magnet does not exert a torque on itself due to its own field.
R: One element of a current-carrying non-straight wire exert a force on another element of the same wire.
View Solution