The outer faces of a rectangular slab made of equal thickness of iron and brass are maintained at 100∘C and 0∘C respectively. The temperature at the interface is (Thermal conductivity of iron and brass are 0.2 and 0.3 respectively)
100∘C
40∘C
50∘C
70∘C
The correct Answer is:B
To solve the problem, we need to find the temperature at the interface of two materials (iron and brass) that are in thermal contact, given their thermal conductivities and the temperatures at their outer faces.
1. Identify the Given Information:
- Temperature at the outer face of iron, T1=100∘C
- Temperature at the outer face of brass, T2=0∘C
- Thermal conductivity of iron, Ki=0.2W/m°C
- Thermal conductivity of brass, Kb=0.3W/m°C
- Thickness of both materials is equal, denoted as Δx.
2. Set Up the Heat Flow Equation:
Since the heat flow through both materials is the same at steady state, we can write:
KiA(T1−T)Δx=KbA(T−T2)Δx
Here, A is the cross-sectional area, and T is the temperature at the interface.
3. Simplify the Equation:
Since the area A and thickness Δx are the same for both materials, they can be canceled out from the equation:
Ki(T1−T)=Kb(T−T2)
4. Substitute the Known Values:
Plugging in the values of Ki, Kb, T1, and T2:
0.2(100−T)=0.3(T−0)
5. Expand and Rearrange the Equation:
Expanding both sides gives:
20−0.2T=0.3T
Rearranging the equation:
20=0.2T+0.3T
20=0.5T
6. Solve for T:
Dividing both sides by 0.5:
T=200.5=40∘C
Final Answer:
The temperature at the interface is T=40∘C.
---
- Temperature at the outer face of iron, T1=100∘C
- Temperature at the outer face of brass, T2=0∘C
- Thermal conductivity of iron, Ki=0.2W/m°C
- Thermal conductivity of brass, Kb=0.3W/m°C
- Thickness of both materials is equal, denoted as Δx.
Since the heat flow through both materials is the same at steady state, we can write:
KiA(T1−T)Δx=KbA(T−T2)Δx
Here, A is the cross-sectional area, and T is the temperature at the interface.
Since the area A and thickness Δx are the same for both materials, they can be canceled out from the equation:
Ki(T1−T)=Kb(T−T2)
Plugging in the values of Ki, Kb, T1, and T2:
0.2(100−T)=0.3(T−0)
Expanding both sides gives:
20−0.2T=0.3T
Rearranging the equation:
20=0.2T+0.3T
20=0.5T
Dividing both sides by 0.5:
T=200.5=40∘C
The temperature at the interface is T=40∘C.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTEChapter:THERMAL PROPERTIES OF MATTERExercise:Assignment (Section-B) Objective Type questions (one option is correct)
Explore 15 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTEChapter:THERMAL PROPERTIES OF MATTERExercise:Assignment (Section-C) Objective Type questions (More than one option are correct)
Explore 13 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTEChapter:THERMAL PROPERTIES OF MATTERExercise:Try Youself
Explore 16 Videos
- TEST 9Book:AAKASH INSTITUTEChapter:TEST 9Exercise:EXAMPLE
Explore 61 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTEChapter:THERMODYNAMICSExercise:ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
Explore 10 Videos
Similar Questions
The outer face of a rectangular slab of equal thickness of iron and brass are maintained at 100∘C and 0∘C, respectively. Find the temperature of the interface. The conductivities of iron and brass are 14 and 126Wm−1K−1 respectively.
View Solution+2.0 -0.0 An engineer joined a rod in which 50 cm is copper and 100 cm is steel from end to end together. Both have the circular cross-section with diameter 3 cm. If the free end of copper and steel are maintained at the temperature 100°C and 0°C respectively. Determine the temperature of the copper-steel junction. (Assume the thermal conductivity of copper and steel are 386 J/m - 5-°C. 46 J/m - 5-°C respectively) 50 cm 100 cm 100°C Copper Steel 0°C
View Solution
Knowledge Check
Two ends of a conducting rod of varying cross-section are maintained at 200∘Cand0∘C respectively. In steady state :
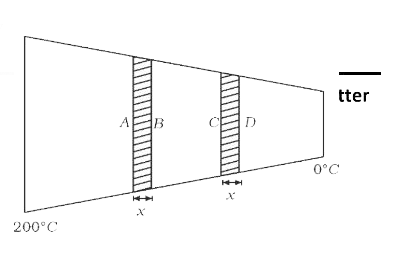 Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.Two ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:
 Atemperature differences across ABandCD are equalBtemperature difference aross AB is greater than that across CDCtemperature difference aross AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across ABandCD are equalBtemperature difference aross AB is greater than that across CDCtemperature difference aross AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.Three metal rods made of copper, aluminium and brass, each 20cm long 4cm in diameter, are placed end to end with aluminium between the other two. The free ends of copper and brass are maintained at 100 and 0∘C respectively. Assume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. The approximately equilibrium temperatures of the copper-aluminiu and aluminium-brass junctions are respectively.
 A68∘C and 75∘CB75∘C and 68∘CC57∘C and 86∘CD86∘ and 57∘C
A68∘C and 75∘CB75∘C and 68∘CC57∘C and 86∘CD86∘ and 57∘C
A composite wall of area A is made of equal thickness of lead and iron having thermal conductivities K and 2K, respectively. The temperature on the two sides of the composite wall are 100∘C and 0∘C with the layer on the hotter side. Calculate the steady -state temperature of the lead-iron interface.
View SolutionAssume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. Three metal rods made of copper, aluminium and brass are each 15 cm long and 2 cm in diameter. These rods are placed end to end, with aluminium between the other two. The free ends of the copper and brass rods are maintained at 100∘C and 0∘C respectively. The system is allowed to reach the steady state condition. Assume there is no loss of heat anywhere.
Under steady state condition the equilibrium temperature of the copper aluminium junction will be
View SolutionAssume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. Three metal rods made of copper, aluminium and brass are each 15 cm long and 2 cm in diameter. These rods are placed end to end, with aluminium between the other two. The free ends of the copper and brass rods are maintained at 100∘C and 0∘C respectively. The system is allowed to reach the steady state condition. Assume there is no loss of heat anywhere.
When steady state condition is reached everywhere, which of the following statement is true?
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is

View SolutionThree rods of copper, brass and steel are welded togeher to from a Y -shaped structure. Area of cross-section of each rod =4cm2. End of copper rod is maintained at 100∘C whereas the ends of brass and steel are at 0∘C . Lengths of copper, brass and steel rods are 46, 13 and 12 cm respectively. The rods are thermally insulated from surroundings except at ends. Thermal conductivities of copper, brass and steel are 0.92,0.26 and 0.12 CGS units respectively. Rate of heat flow through copper rod is
View Solution

