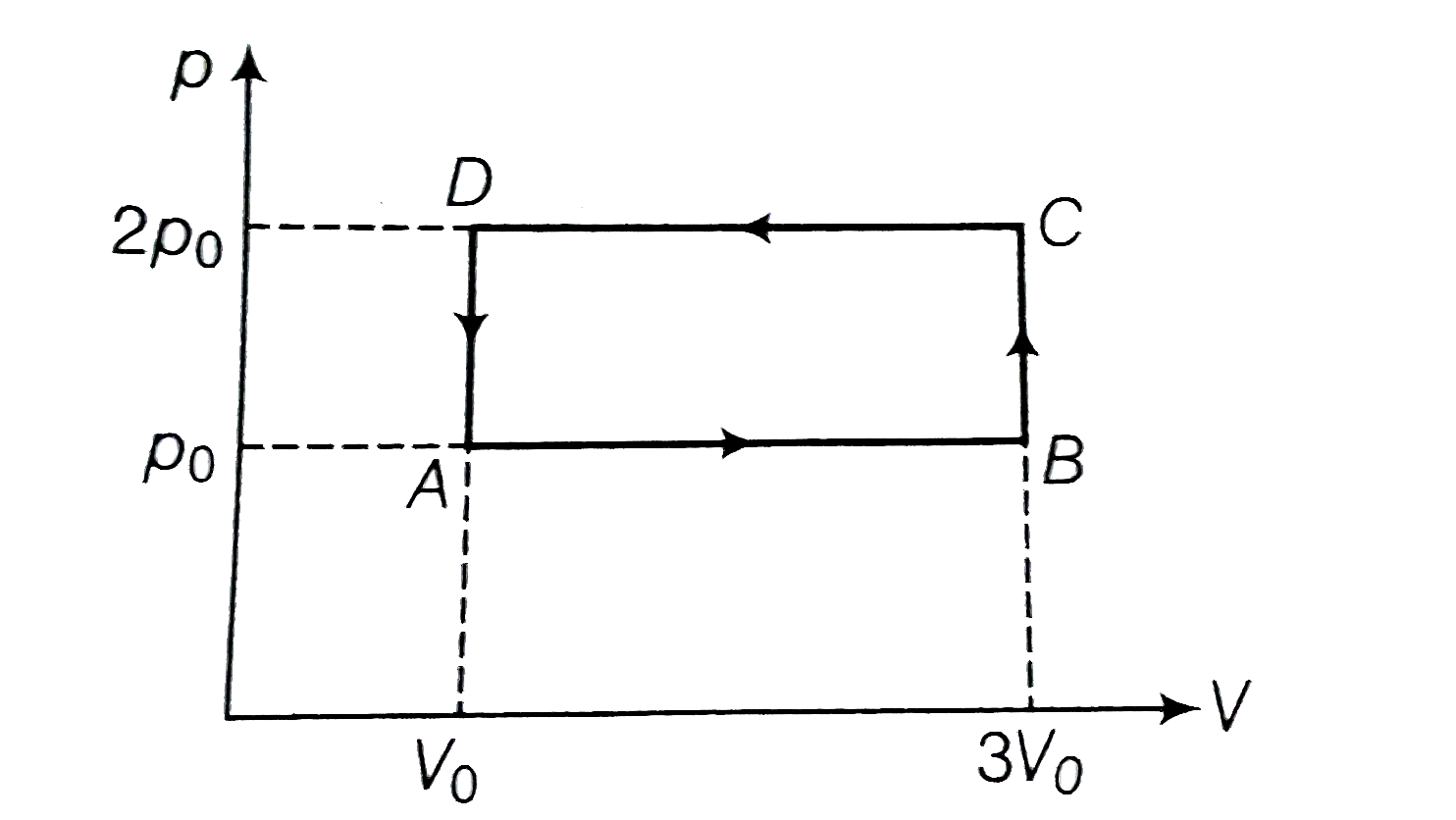
An ideal gas undergoes a cyclic process as shown. Part of the process ab is isothermal expansion and work done by the gas in this expansion is 700 J. in adiabatic expansion be it again does 400 J work. If it rejects 100 J heat when it returns to a from c via b' then find efficiency of the cycle.
Video Solution
Text Solution
ab is an isothermal process, therefore ΔUab=0 ltBrgt Now from first law of thermodynamics
Qab=Wab=700J . . . . (i)
Again bc is an adiabatic process, therefore Qbc=0
as given, Wbc=400J
therefore
ΔUbc=−Wbc=−400J
Now for the complete cycle, ΔU=0
⇒ΔUab+ΔUbc+ΔUcca=0
 .
.
From first law of thermodynamics
Qab+Qbc+Qca=Wab+Wbc+Wca
Substituting values from above, 700+0−100=700+400+ΔWca
⇒ΔWca=−500J
This negative sign indicates that the work is done on the gas.
Now net work done on the gas
ΔW≠t=Wab+Wbc+Wca=[700+400+500]J=600J
total heat supplied to the gas during the cycle
ϕ⊃=700J
η=ΔWnetQsup×100=600700×100=85.71%.
|
Similar Questions
Knowledge Check
A gas undergoes a cyclic process ABCDA as shown in the figure. The part ABC of process is semicircular. The work done by the gas is
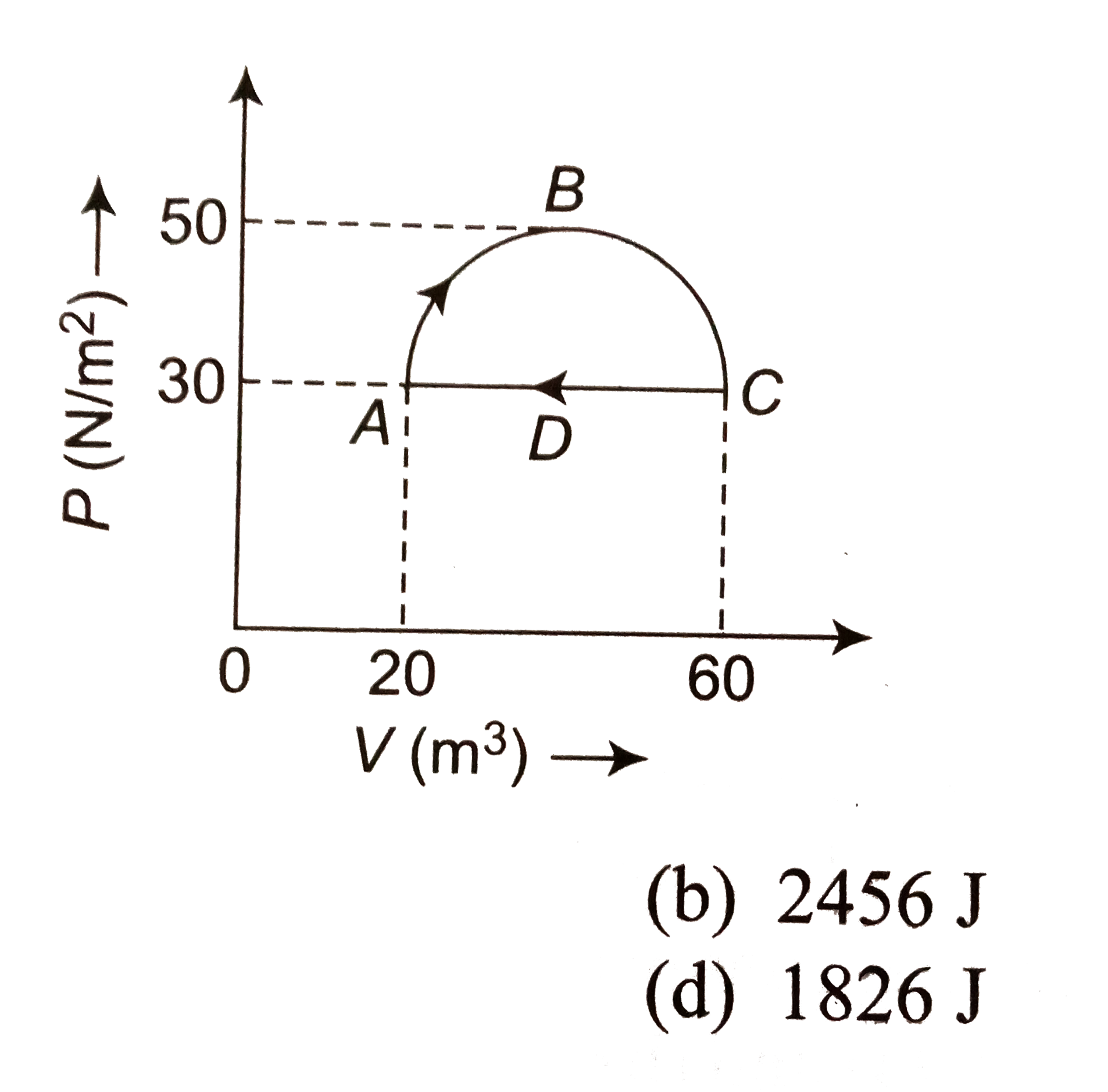 A400πJB2456JC200πD1826J
A400πJB2456JC200πD1826JAn ideal gas undergoes a cyclic process whose indicator diagram is as shown in the figure. Find the work done by the gas in 1 complete cycle.
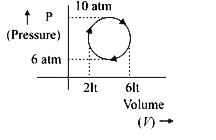 A4π lt-atmB16lt - atmC8π lt - atmD16π lt - atm
A4π lt-atmB16lt - atmC8π lt - atmD16π lt - atmTwo moles of helium gas undergo a cyclic process as shown in figure. Assuming the gas to be ideal. The net work done by the gas is
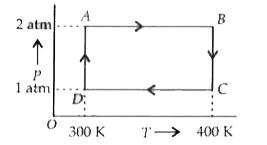 A200 Rln2B100 Rln2C300 Rln2D400 Rln2
A200 Rln2B100 Rln2C300 Rln2D400 Rln2
An ideal gas receives 10J of heat in a reversible isothermal expansion. Then the work done by the gas:
View SolutionAn ideal gas undergoes cyclic process ACBC as shown is given PV diagram
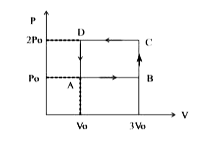
The amount of work done by the gas is
View SolutionTwo moles of an ideal gas are undergone a cyclic process 1-2-3-1. If net heat exchange in the process is 300J, the work done by the gas in the process 2-3 is

View SolutionAn ideal monoatomic gas undergoes a cyclic process ABCA as shown in the figure. The ratio of heat absorbed during AB to the work done on the gas during BC id
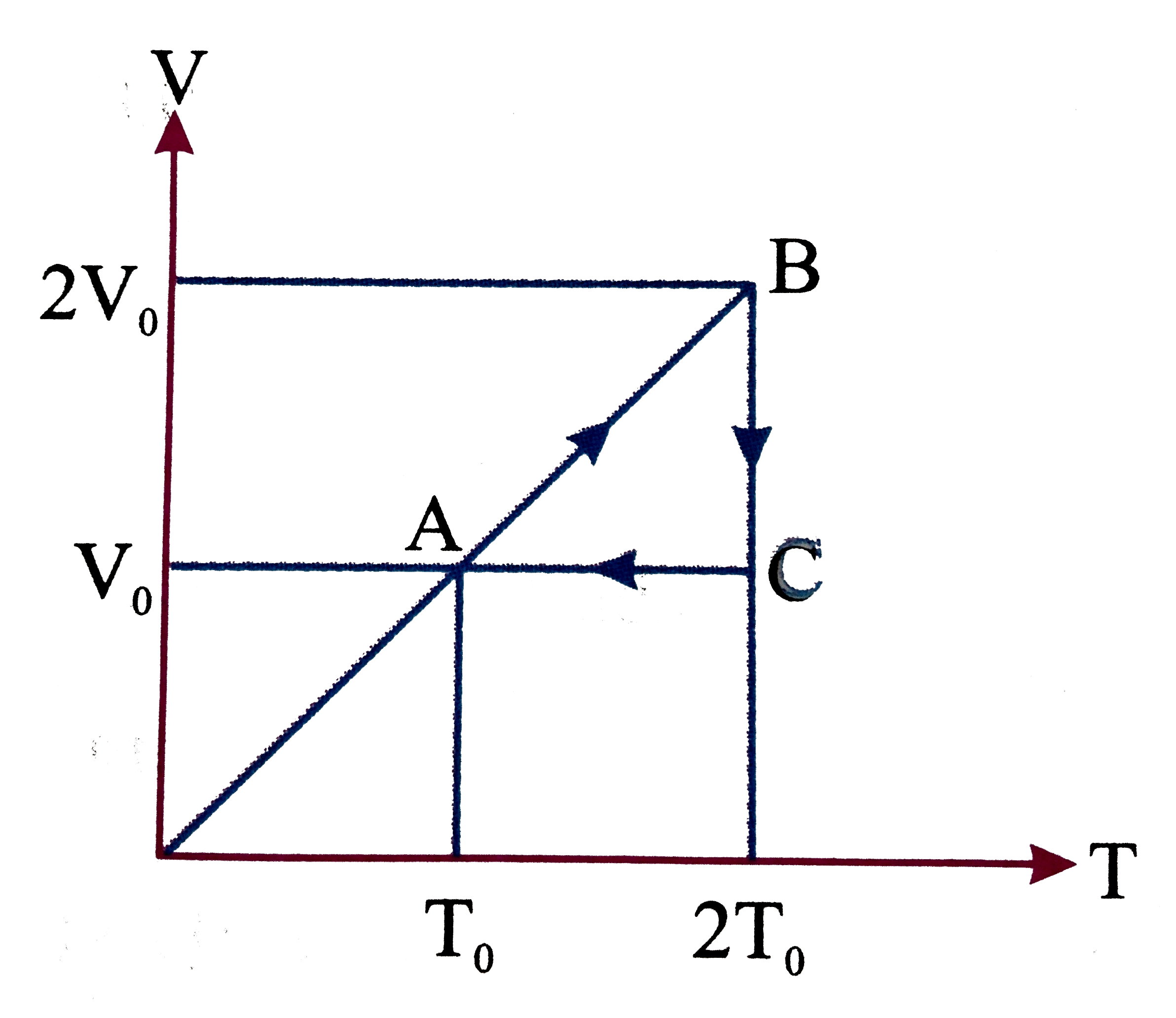
View SolutionTwo moles of an ideal monoatomic gas undergoes a cyclic process ABCA as shown in V-T diagram below:

Work done by the gas during the entire cycle is :
View Solution