A spring mass system osciallates with a time period 7s. The entiresystem is immersed in a liquid whose density at halt that of the material of the block. Find the new time period ( in s ) of osciallations.
The correct Answer is:7
To solve the problem of finding the new time period of a spring-mass system immersed in a liquid, we can follow these steps:
1. Understand the Initial Conditions:
- The initial time period T0 of the spring-mass system is given as 7 s.
- The density of the liquid ρL is half that of the density of the block ρB, i.e., ρL=12ρB.
2. Identify the Forces Acting on the Block:
- When the block is immersed in the liquid, three forces act on it:
- The gravitational force Fg=mg acting downwards.
- The buoyant force Fb=ρLVg acting upwards, where V is the volume of the block.
- The spring force Fs=−kx acting upwards when the block is displaced.
3. Calculate the Effective Weight of the Block:
- The effective weight Weff of the block when submerged is given by:
Weff=Fg−Fb=mg−ρLVg
- Since m=ρBV, we can substitute:
Weff=ρBVg−ρLVg=Vg(ρB−ρL)
- Substituting ρL=12ρB:
Weff=Vg(ρB−12ρB)=Vg(12ρB)
4. Determine the New Effective Mass:
- The effective mass m′ that contributes to the oscillation is now half of the original mass:
m′=12m=12ρBV
5. Relate the New Time Period to the Original Time Period:
- The time period of oscillation for a spring-mass system is given by:
T=2π√mk
- The new time period T′ can be expressed as:
T′=2π√m′k=2π√12mk=2π√m2k=T0√2
- Since T0=7 s:
T′=7√2≈4.95 s
6. Final Result:
- The new time period of oscillation when the spring-mass system is immersed in the liquid is approximately 4.95 s.
Summary:
The new time period of the oscillations of the spring-mass system immersed in the liquid is approximately 4.95 s.
- The initial time period T0 of the spring-mass system is given as 7 s.
- The density of the liquid ρL is half that of the density of the block ρB, i.e., ρL=12ρB.
- When the block is immersed in the liquid, three forces act on it:
- The gravitational force Fg=mg acting downwards.
- The buoyant force Fb=ρLVg acting upwards, where V is the volume of the block.
- The spring force Fs=−kx acting upwards when the block is displaced.
- The effective weight Weff of the block when submerged is given by:
Weff=Fg−Fb=mg−ρLVg
- Since m=ρBV, we can substitute:
Weff=ρBVg−ρLVg=Vg(ρB−ρL)
- Substituting ρL=12ρB:
Weff=Vg(ρB−12ρB)=Vg(12ρB)
- The effective mass m′ that contributes to the oscillation is now half of the original mass:
m′=12m=12ρBV
- The time period of oscillation for a spring-mass system is given by:
T=2π√mk
- The new time period T′ can be expressed as:
T′=2π√m′k=2π√12mk=2π√m2k=T0√2
- Since T0=7 s:
T′=7√2≈4.95 s
- The new time period of oscillation when the spring-mass system is immersed in the liquid is approximately 4.95 s.
The new time period of the oscillations of the spring-mass system immersed in the liquid is approximately 4.95 s.
Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )
Explore 3 Videos
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
Explore 7 Videos
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION-F( MATRIX MATCH TYPE QUESTIONS) )
Explore 3 Videos
- NUCLEIBook:AAKASH INSTITUTEChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTEChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 5 Videos
Similar Questions
Knowledge Check
A simple pendulum has a time period T. The pendulum is completely immersed in a non-viscous liquid whose density is one-tenth of that of the material of the bob. The time period of the pendulum immersed in liquid is
ATB√910TC√109TDT10A simple pendulum oscillating in air has a time period of √3s. Now the bob of the pendulum is completely immersed in a non-viscous liquid whose density is equal to 14th that of the material of the bob. The new time period of simple pendulum will be
A√2sB√3sC2sD√72sFind the time period of SHM of the block of mass M
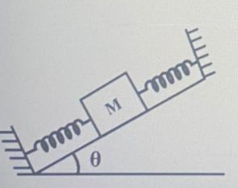 AT=2π√M2KBT=2π√MKCT=2π√2MKDT=2π√M4K
AT=2π√M2KBT=2π√MKCT=2π√2MKDT=2π√M4K
A simple pendulum has time period 2s in air. If the whole arrangement is placed in a non viscous liquid whose density is 1/2 times the density of bob, find the time period of oscillation in liquid.
View SolutionA mass suspended from a spring of spring constant k is made to oscillate with a time period T. Now, the spring is cut into three equal parts and the mass is suspended from one of the parts. What will be the new time period of oscillations?
View SolutionA simple pendulum has a time period T in vacuum. Its time period when it is completely immersed in a liquid of density one-eight of the density of material of the bob is
View SolutionThe periodic time of a simple pendulum, oscillating in air is T. But if the bob of the simple pendulum is completely immersed in a nonviscous liquid, whose density is 120 th of the material of the bob, then its new period will be
View SolutionA simple pendulum has a time period T in vacuum. Its time period when it is completely immersed in a liquid of density one-eight of the density of material of the bob is
View Solution



