What will be the time period of a pendulum which beats seconds ( i.e.,

If the time period of a pendulum is $1 sec$ , then what is the length of the pendulum at point of intersection of $l - T$ and $l - T^{2}$ graph.

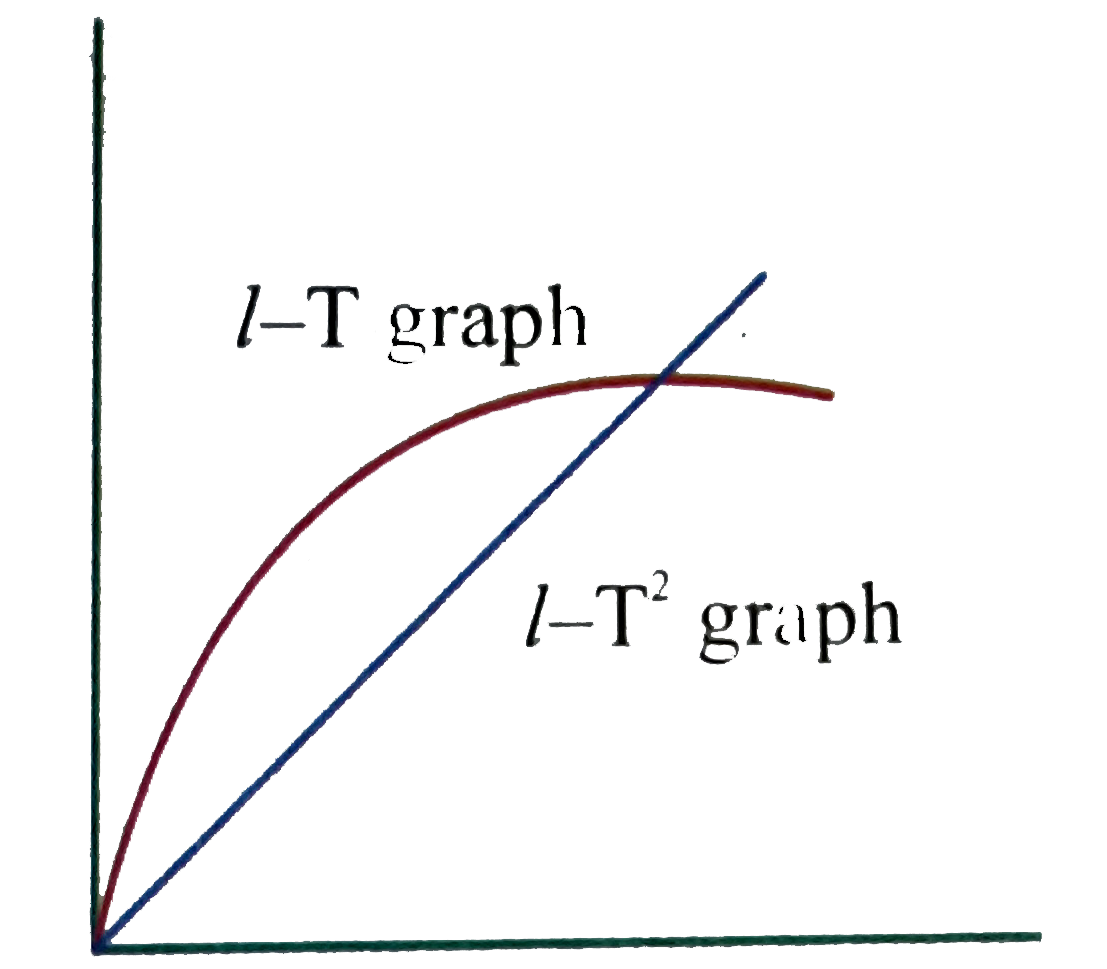A $25 c m$
B $21 c m$
C $22 c m$
D $27 c m$
If the time period of a simple pendulum is $T = 2 π \sqrt{l / g}$ , then the fractional error in acceleration due to gravity is
A $\frac{4 π^{2} Δ l}{Δ T^{2}}$
B $\frac{Δ l}{l} - 2 \frac{Δ l}{T}$
C $\frac{Δ l}{l} + 2 \frac{Δ T}{T}$
DNone of these
Statement-1: The time period of a simple pendulum on a satellite orbiting the earth is infinity
Because
Statement-2: Effective value of g in orbiting satellite is zero and $T = 2 π \sqrt{\frac{l}{g}}$
AStatement-1 is True, Statement-2 is true, Statement -2 is a correct explanation for statement-1
BStatement-1 is true, statement-2 is true, statement-2 is not a correct explanation for statement-1
CStatement-1 is true, Statement -2 is false
DStatement -1 is false, statement-2 is true

What will be the time period of a pendulum which beats seconds ( i.e.,it passes through the mean position after every one second ) it its length is doubled ?
Hint $: T = 2 π \sqrt{\frac{L}{g}} = 2$ ....(i)
$T' = 2 π \sqrt{\frac{2 L}{g}}$
Fin $T'$ using equation (i)