STATEMENT -1 : A small object if released from rest from a point upon the axis of a large mass circular ring, but very near to the centre of ring, will perform SHM.
and
STATEMENT -2 : The gravitational field of mass circular ring changes non-linearly with the axial distance, near the centre.
Statement 1- True, Statement -2 is True, Statement -2 is a correct explanation for Statement -1
Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1
Statement -1 is True, Statement -2 is False
Statement -1 is False, Statement -2 is True
The correct Answer is:C
Step by step video, text & image solution for STATEMENT -1 : A small object if released from rest from a point upon the axis of a large mass circular ring, but very near to the centre of ring, will perform SHM. and STATEMENT -2 : The gravitational field of mass circular ring changes non-linearly with the axial distance, near the centre. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -F (Matrix - Match Type Questions)
9 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -G (Integer Answer Type Questions)
6 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -D (Linked Comprehension Type Questions)
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
A particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionMass of 10 kg is distributed uniformly over a ring of radius 1m. Find the gravitational potential at a point lies on the axis of the ring at a distance of 1m from the centre.
View Solution
Knowledge Check
A small element l cut from a circular ring of radius a and λ charge per unit length. The net electric field at the centre of ring is
AzeroBλl4πε0a2C∞Dλ4πεlAn electron released on the axis of a positively charged ring at a large distance from the centre will
ANot moveBDo oscillatory motionCDo SHMDDo non-periodic motionSTATEMENT -1 : Kepler's second law is the consequence of law of conservation of angular momentum.
STATEMENT -2 : In planetary motion, the momentum, angular momentum and mechanical energy is conserved.
STATEMENT -3 : The gravitational field of a circular ring is maximum at a point upon axis at distance R√2 from the centre, where R is the radius of ring.AT F TBT F FCF F FDT T T
A point P lies on the axis of a fixed ring of mass M and radius a, at a distance a from its centre C. A small particle starts from P and reaches C under gravitational attraction only. Its speed at C will be.
View SolutionMass of 20 kg is distributed uniformly over a ring of radius 2m. Find the the grvitational field at a point lies an th axis of the ring at a distance of 2√3 m from the centre.
View SolutionA mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass M is
View SolutionSTATEMENT 1: When a negative charge -q is released at a distance R from the centre and along the axis of a uniformly and positvely charged fixed ring of radius R, the negative charge does oscillation but not SHM. STATEMENT 2: The force on negative charge is always towards the centre of the ring but it is not proportional to the displacement from the centre of the ring.
View SolutionA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
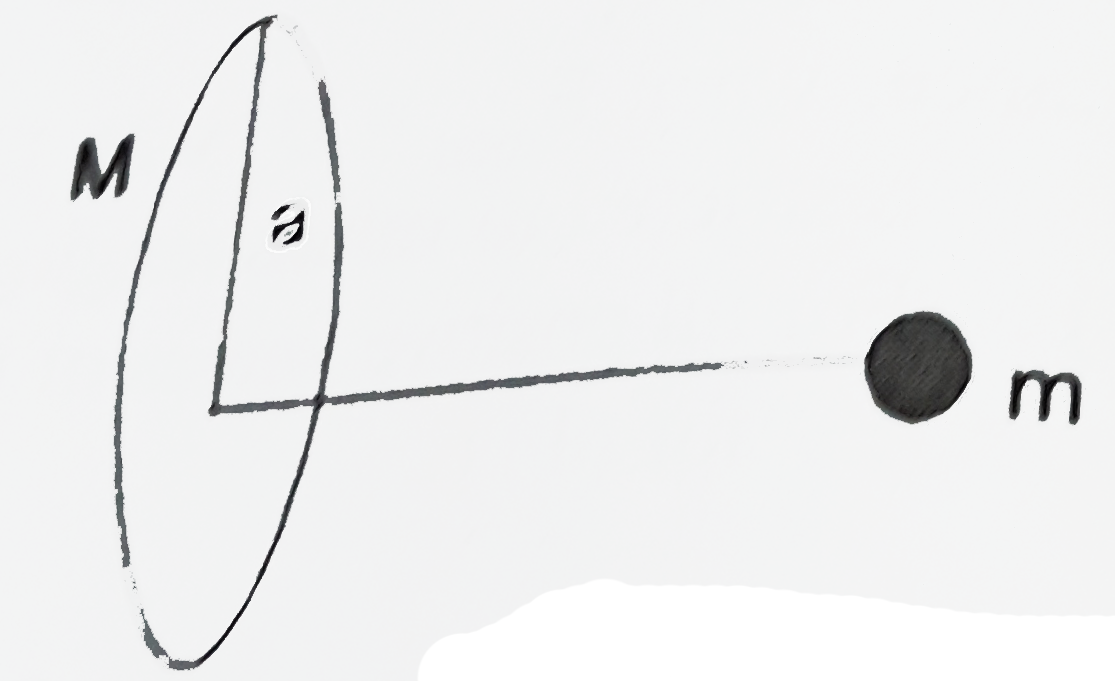
if x<<a, the particle of mass m will:
View Solution
