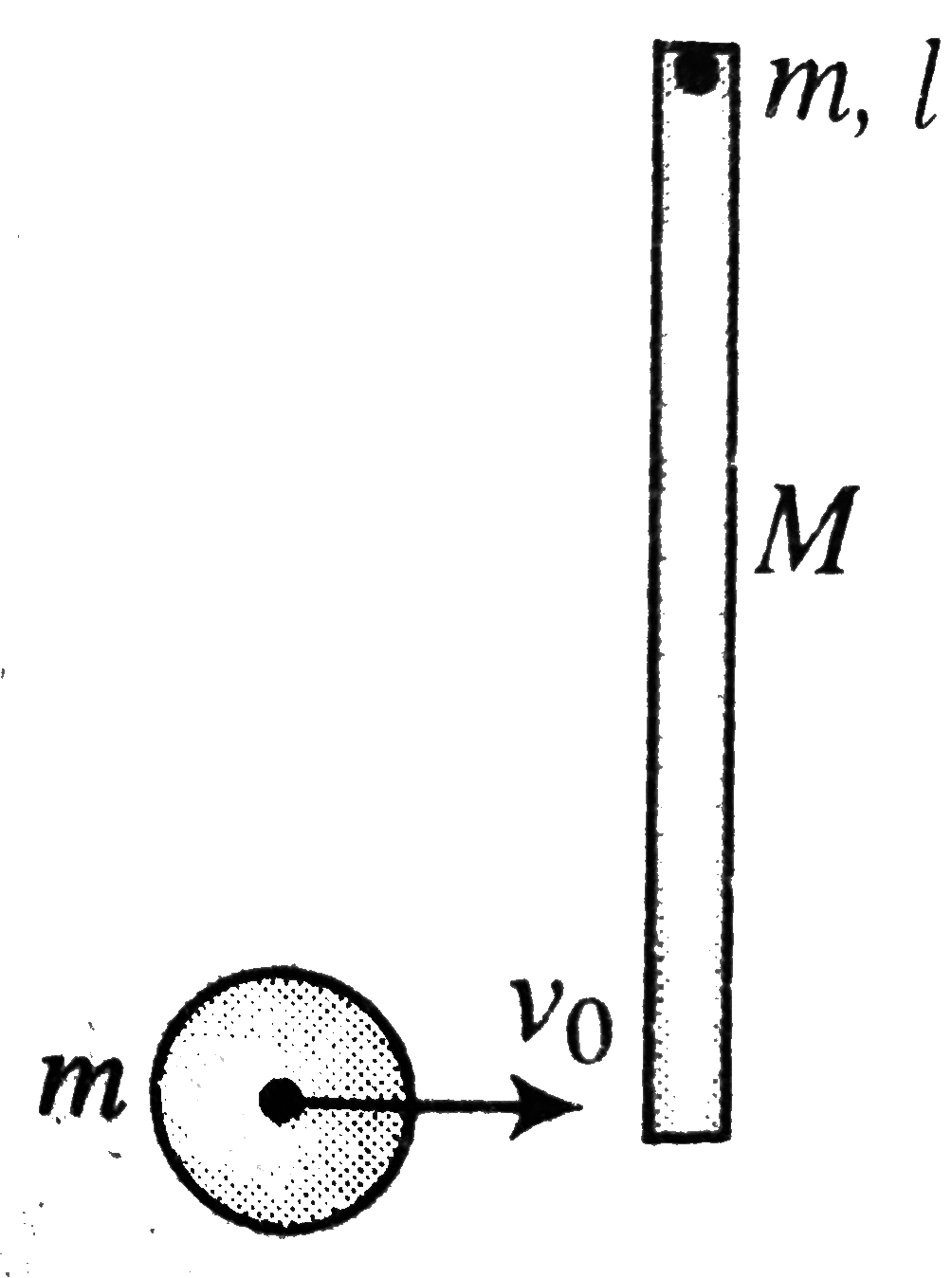
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision.
Let us assume that speed of centre of mass of rod be v0 and angular speed about centre of mass be ω immediately after collision.

Taking the ball and rod to be part of a combined system, so for our system ∑Fext=0. So momentum can be conserved.
(a)∴mv0=MV⇒v=mMv0..........(1)
∑τ=0 about centre of rod. So conserving angular momentum
mv0⋅L2=ICM⋅ω⇒mv0L2=ML212ω
∴ω=6mMv0L..........(2)
Since the collision is perfectly elastic, K.E. of system will remain conserved.
12mv20=12MV2+12IC.M.⋅ω2 [Replacing the values of v and ω from equation (1) and (2) ]
⇒12mv20=12M(mMv0)2+12⋅ML212×36m2M2v20L2
or 1=mM+3mM=4mM
mM=14
(b) For velocity of any point P to be zero immediately after the collision, the net velocity of point P is
v+ωx=0
∴x=−vω
=−mv0M⋅6mv0ML
∴=−L6
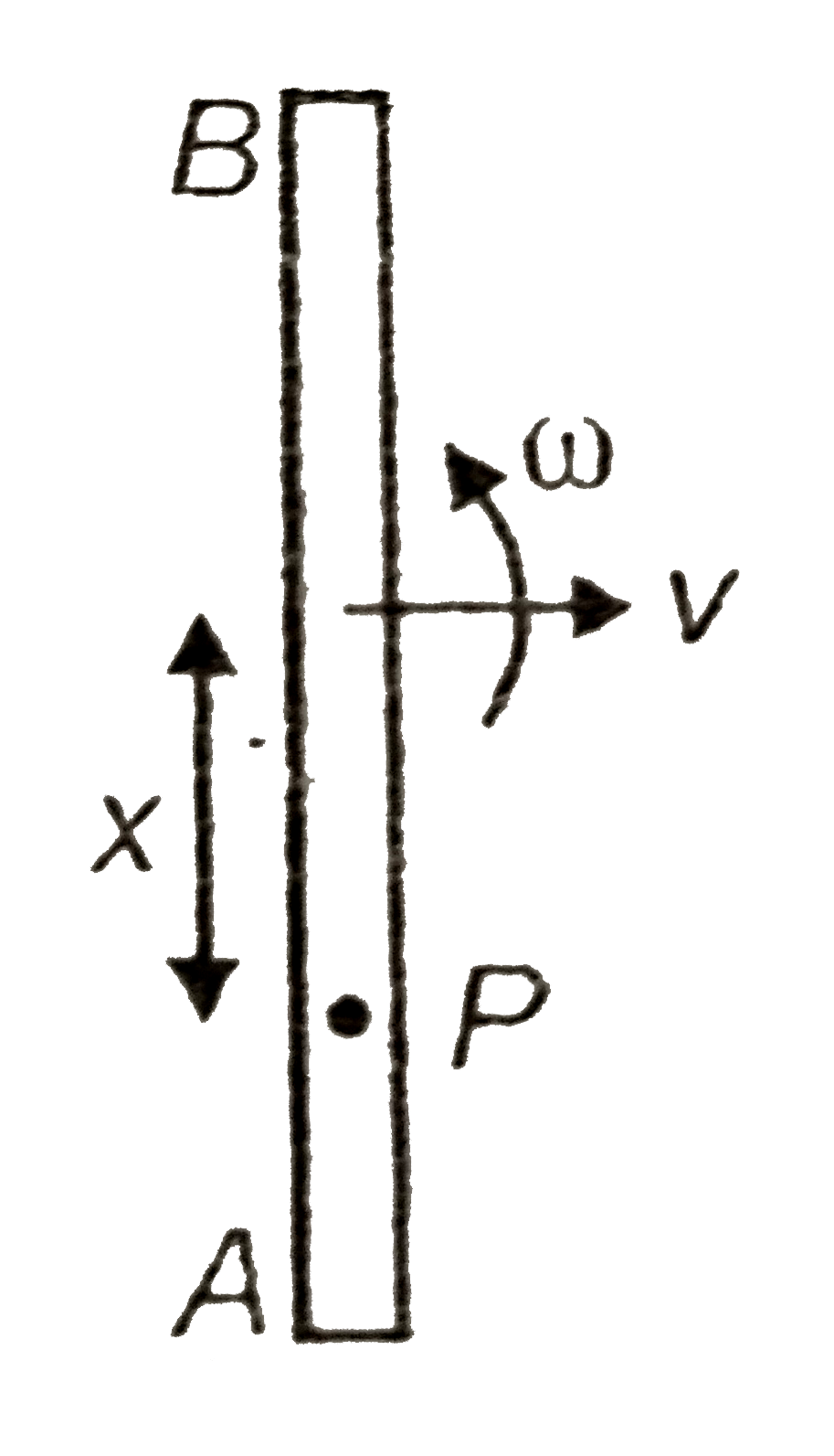
(-ve sign shows that the point will be on opposite side of what we have taken and is quite-logical too)

So, AP=L2+L6=4L6=2L3
(c) Just after collision,
v=mMv0=v04
ω=6mv0ML=3v02L
Since v=ωL6, both the translational speed as well as speed due to rotation will be equal to v=v04 at any time after collision.
After time t=πL3v0
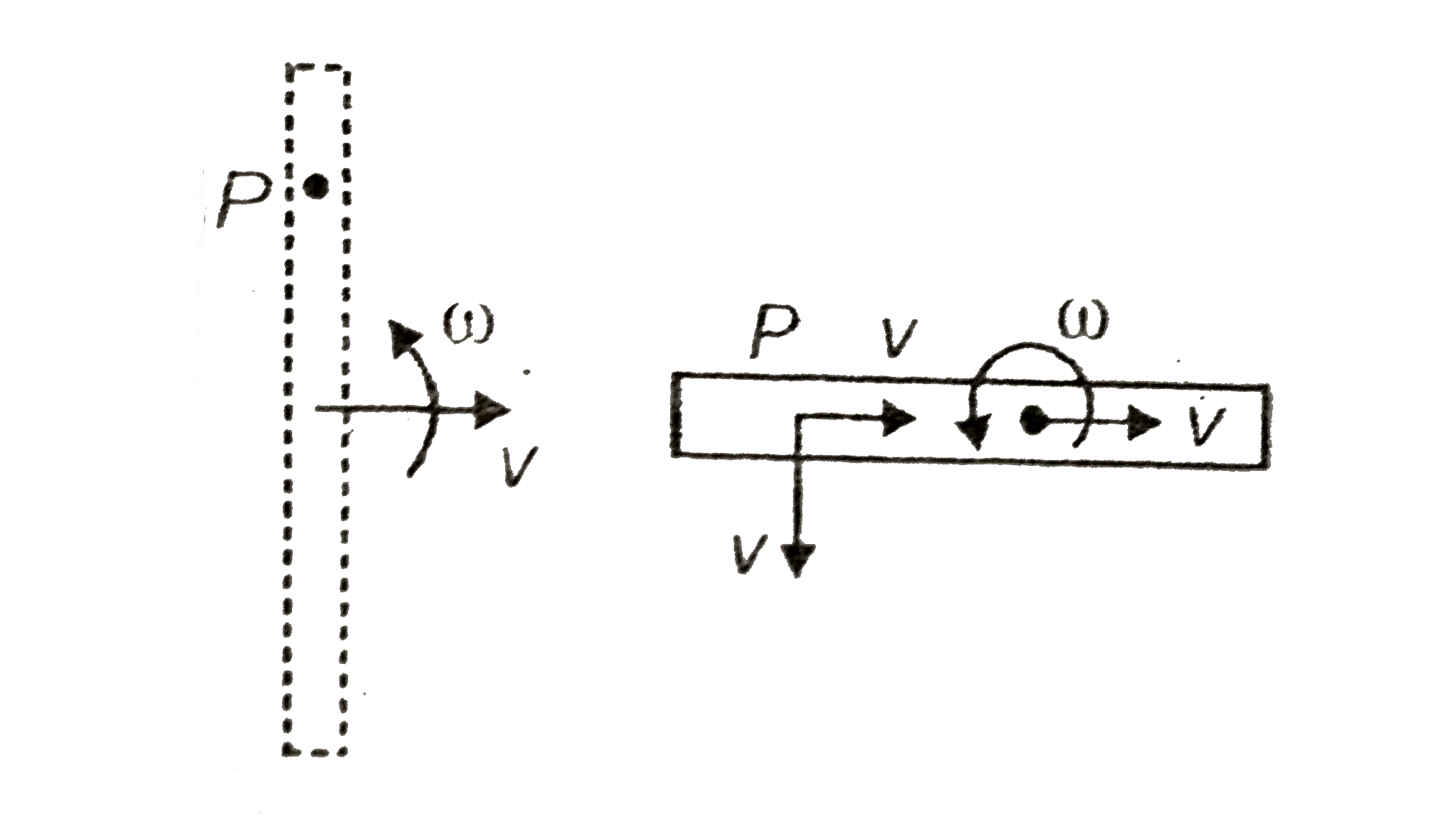
θ=ωt=3v02L×πL3v0=π2
So rad has turned by an angle π2, till that time after collision.
The point P has two velocities one in the direction of motion of cenre of rod and another perpendicular to the rod.
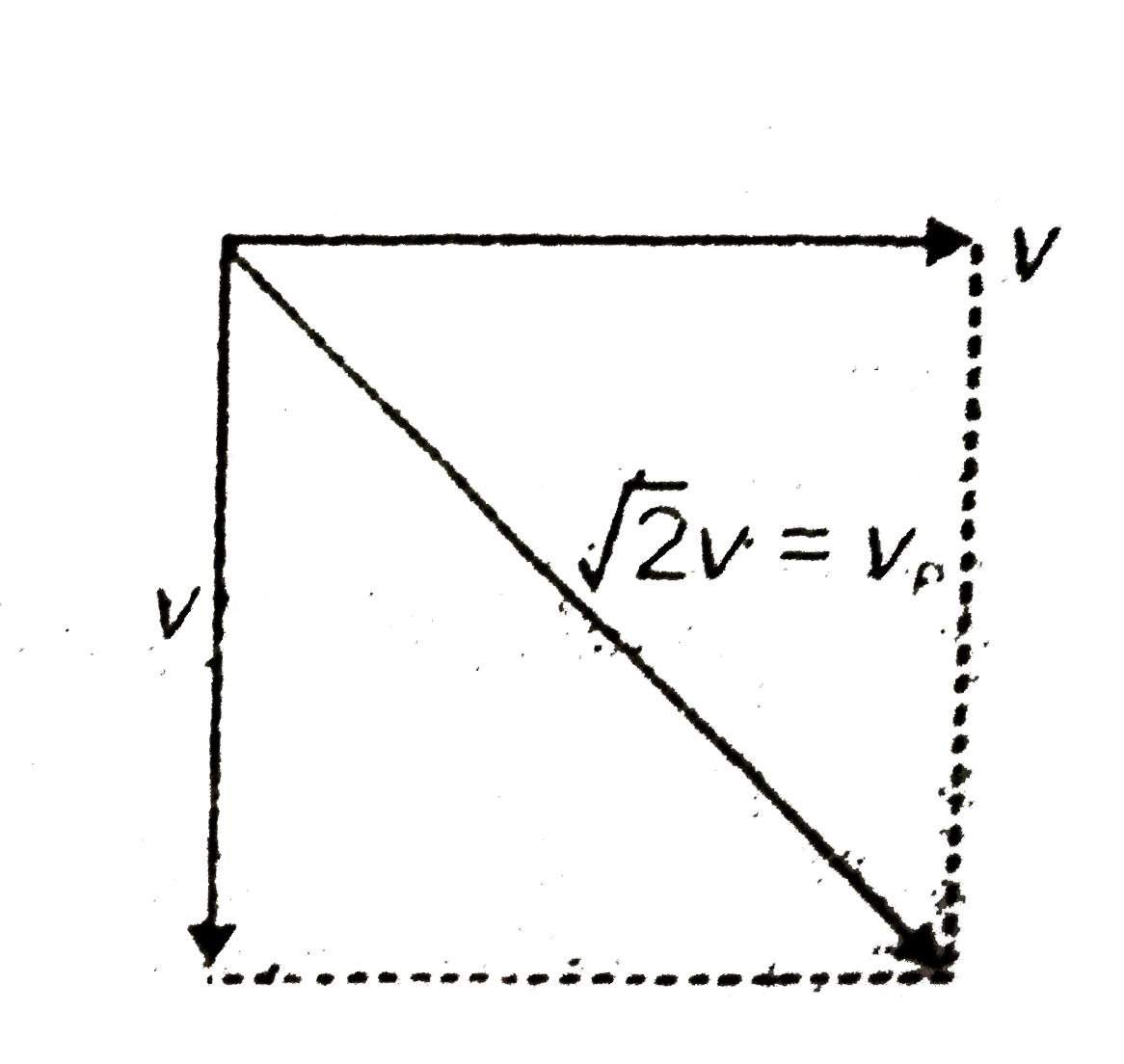
Resultant speed =√v2+v2=v√2=v04√2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Illustration
Explore 4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - A) Objective Type Questions (One option is correct)
Explore 62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTEChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTEChapter:TEST 1Exercise:EXERCISE
Explore 9 Videos
Similar Questions
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m traveling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision the particle comes to rest. Find the ration m/M.
View SolutionA rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with a velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses (mM) is 1x. The value of 'x' will be_____.
View Solution
Knowledge Check
A rod AB of mass M, length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision, the particle comes to rest. The ratio mM is :
Aw2L29v20B9v20w2L2C9v0wLDwL9v0A rod AB of mass M, length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision, the particle comes to rest. The ratio mM is :
Aw2L29v20B9v20w2L2C9v0wLDwL9v0A rod AC of length l and mass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of same mass m moving on the plane with velocity v strikes the rod at point B making angle 37∘ with the rod. The collision is elastic. After collision,
 Athe angular velocity of the rod will be 72/55v/lBthe centre of the rod will travel a distance it πl/3 in the time in which it makes half rotationCimpulse of the impact force is 24mV/55Dnone of these
Athe angular velocity of the rod will be 72/55v/lBthe centre of the rod will travel a distance it πl/3 in the time in which it makes half rotationCimpulse of the impact force is 24mV/55Dnone of these
A rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
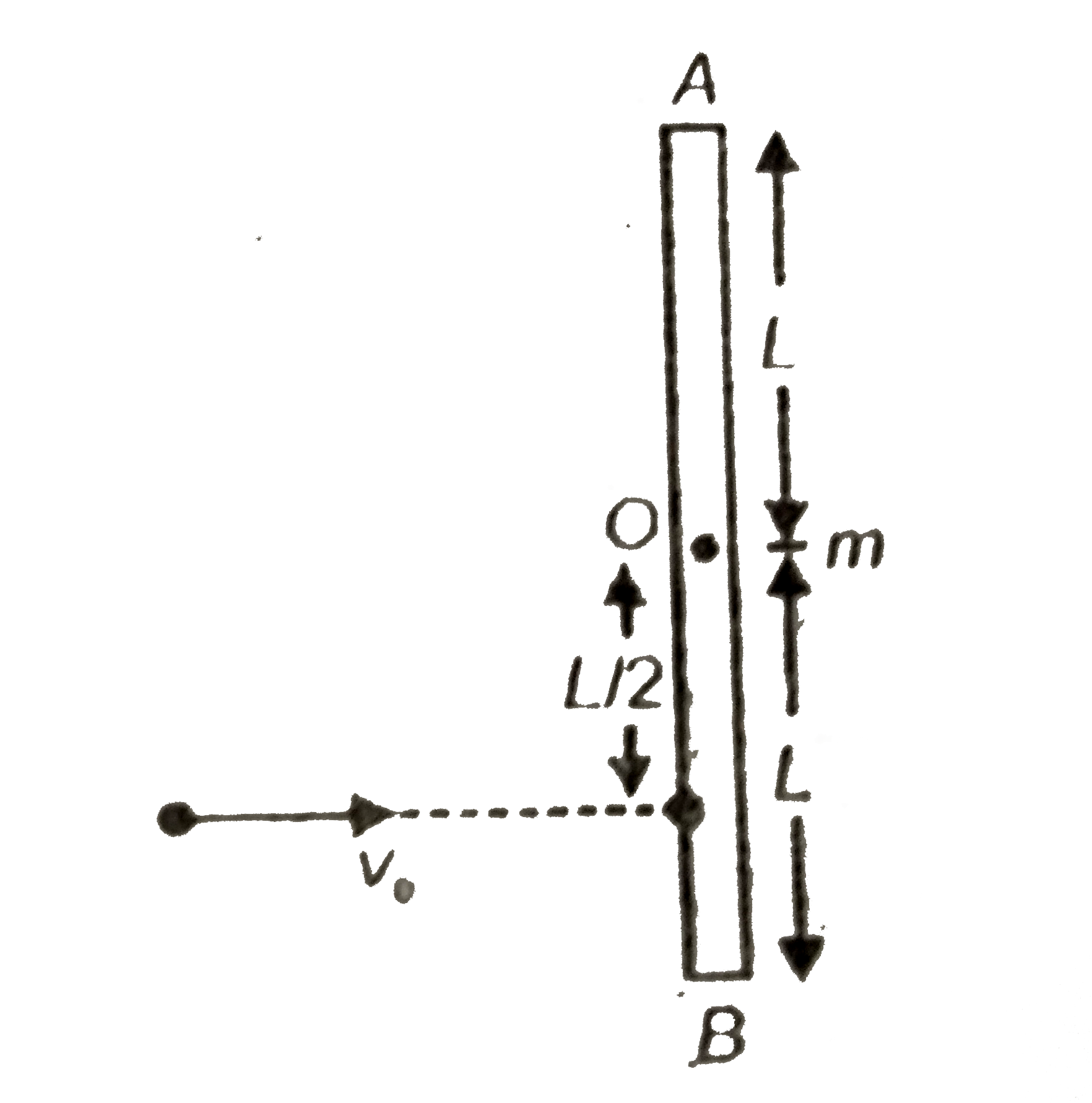
Angular velocity of rod just after collision is
View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA rod of mass m and length L is kept on a frictionless horizontal floor. A particle of same mass m moving perpendicular to the rod with a speed v strikes at the end of the rod. If coefficient of elasticity for the collision is 1 then calculate angular velocity acquired by the rod.
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
View Solution
