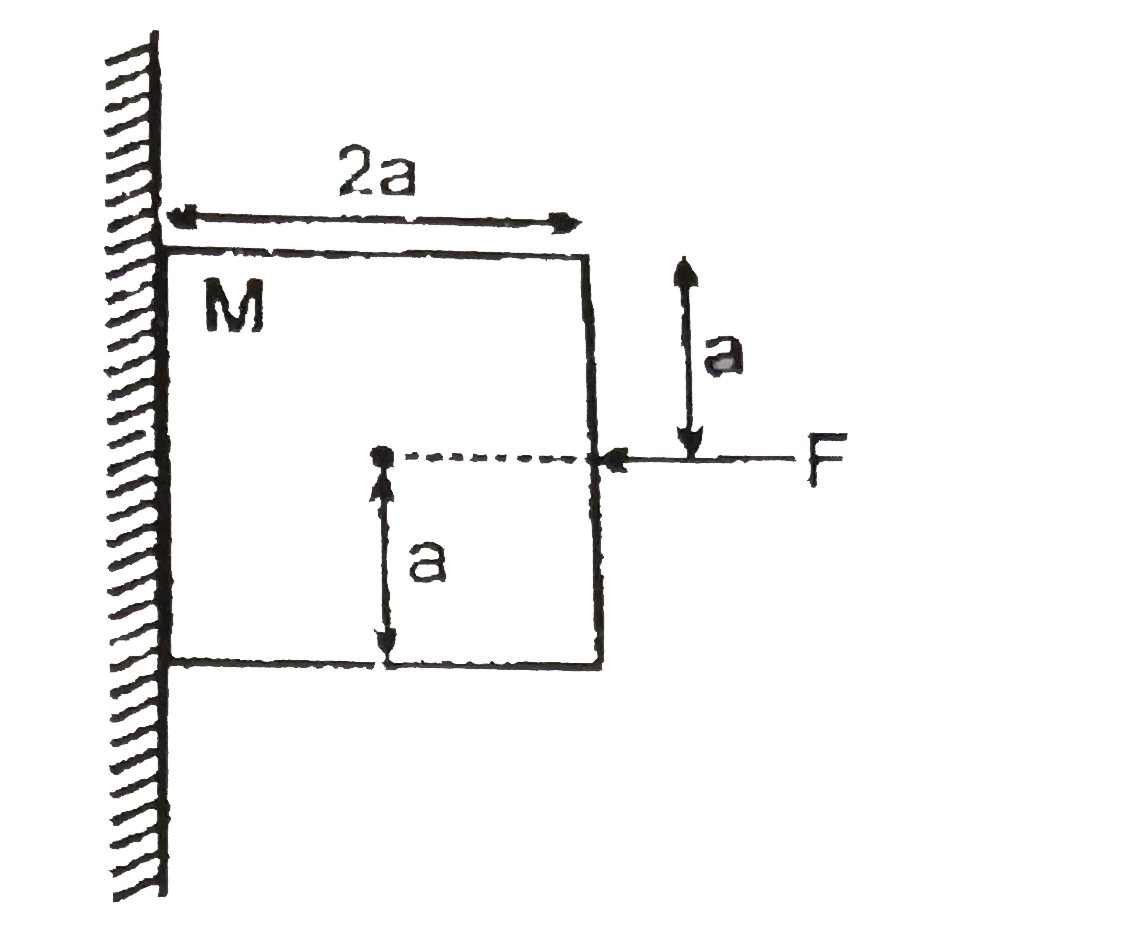
A cubical block of side 'a' is held at rest, against a rough vertical wall by applying a force $F$ acting along the centre. The mass of the block is $m$ . Taking acceleration due to gravity as 'g' , determine
$(i)$ The minimum coefficient of friction between the block and wall
$(i i)$ The torque by normal reaction about the centre of mass

Video Solution

Text Solution

Verified by Experts

The situation is shown in the figure.

Let $C$ be the cenre. For equilirbium of the block
$\sum F_{x} = 0$ , $\sum F_{y} = 0$ , $\sum τ = 0$
$\Rightarrow F - N = 0$ , $f_{s} = m g$ , $f_{s} \times \frac{a}{2} + τ_{N} = 0$
Here, clockwise torque has been taken as negative.
Note: Normal reaction due to the wall $N$ , does not pass through the centre $C$ .
Now, $N = F$
$f_{s} = m g$
$(i)$ As $f_{s} \leq μ N$
$\Rightarrow m g \leq μ F$
or $μ \geq \frac{m g}{F}$
$(i i)$ $- \frac{f_{s} (a)}{2} + τ_{N} = 0$
$τ_{N} = f_{s} \times \frac{a}{2} = m g . \frac{a}{2}$ (in counter clockwise sense)

Updated on:21/07/2023

A block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is $0.5 .$ When

AF = 40 N, friction on the block is 20 N.
BF = 30 N, friction on the block is 10 N.
CC = 20 N, friction on the block is 10 N.
DMinimum value of force F to keep block at rest is 20 N.
A block of mass 'm' is held stationary against a rough wall by applying a force F as shown. Which one of the following statement is incorrect ?

AFriction force $f = m g$
BNormal reaction $N = F$
CF will not produce a torque
DN will not produce any torque
A block weighs W is held against a vertical wall by applying a horizontal force F. The minimum value of F needed to hold the block is
Aless tha W
BEqual to W
CGreater than W
DData is insufficient