Consider the spring block system shown in the figure. Initially block m is in equilibrium. Then block m is displaced b y a small distance h. Find the maximum speed of the block. ltbgt 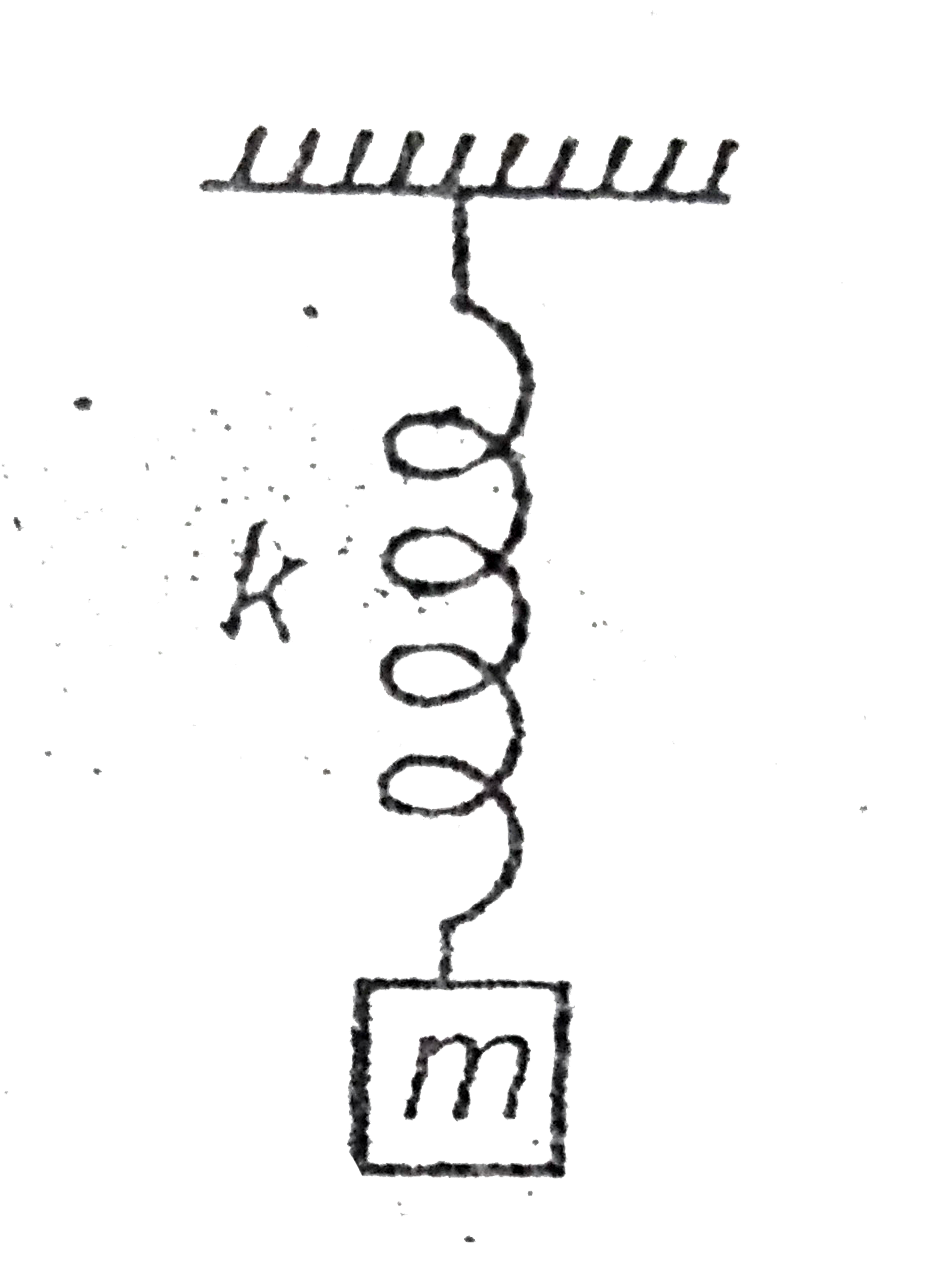
h√km
2h√kh
h√mk
2h√mk
The correct Answer is:A
Step by step video & image solution for Consider the spring block system shown in the figure. Initially block m is in equilibrium. Then block m is displaced b y a small distance h. Find the maximum speed of the block. ltbgt by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)
Explore 16 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-I)
Explore 3 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)
Explore 60 Videos
- WAVESBook:AAKASH INSTITUTEChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
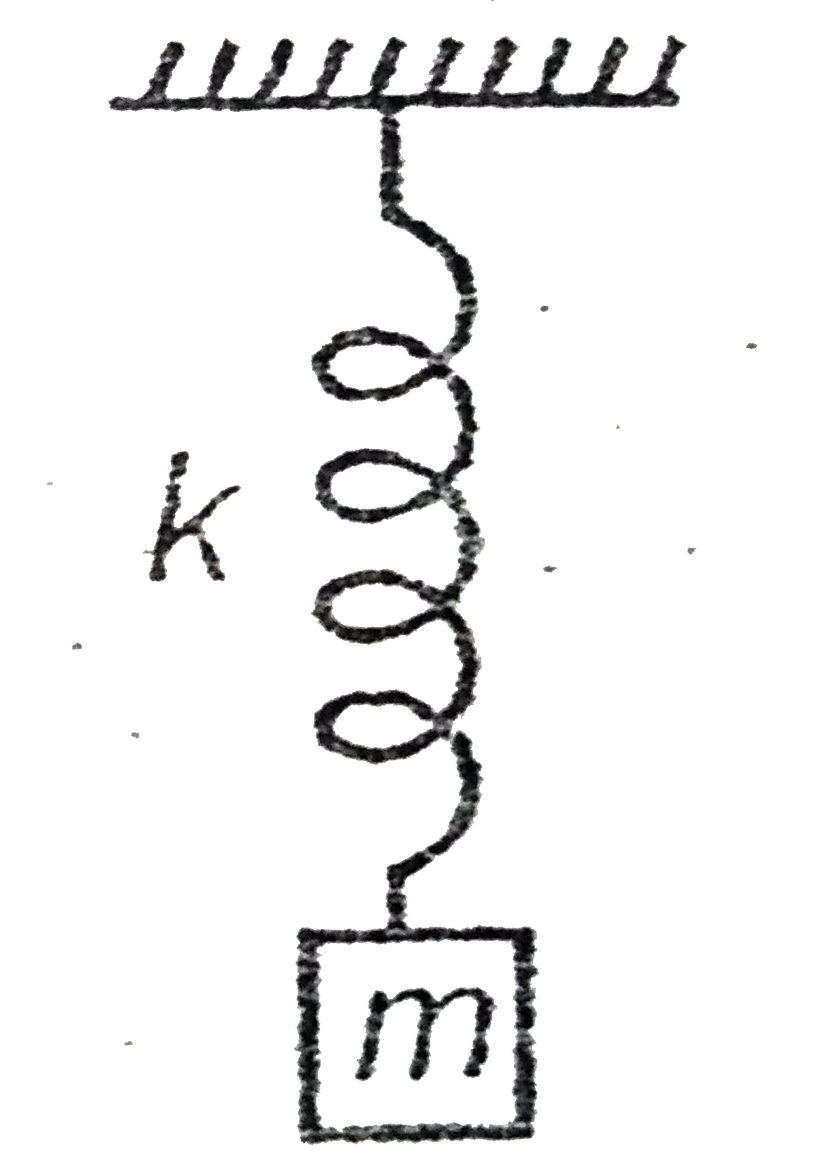
Consider the spring blcok system shoen in the figure initially block m is in equlibrium. An impulse gives the block a velocity v upwards. Find the maximum speed of the block during the motion.
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution
Knowledge Check
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)A constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)
 AThe block will executes SHMBAmplitude of oscillation is F2KCTime period of oscillation is 2π√mkDThe maximum speed of block is √2Fx−kx2m (Here, x=F/k).
AThe block will executes SHMBAmplitude of oscillation is F2KCTime period of oscillation is 2π√mkDThe maximum speed of block is √2Fx−kx2m (Here, x=F/k).
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2km
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

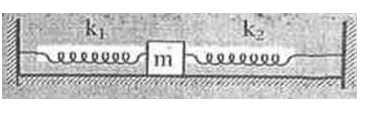
View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
View SolutionFigure shown a spring block system hanging in equilibrium. If a velocity v0 is imparted to the block in downwards direction . Find the amplitude of SHM of the block and the time after which it will reach a point at half the amplitude of block

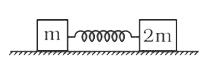
View SolutionA spring is connected between two blocks as shown in the diagram. Initially the blocks are held stationary and suddenly they are released. Find the ratio of maximum kinetic energy with spring compressed the block of mass m to that of mass 2m.
View Solution

