Two particles A and B have the same mass m. A is moving along X-axis with a speed of 5ms−1 and B is at rest. After undergoing a perfectly elastic collision with B, particle A gets scat tered through an angle of 60∘. What is the direction of B, and the speeds of A and B, after the collision ?
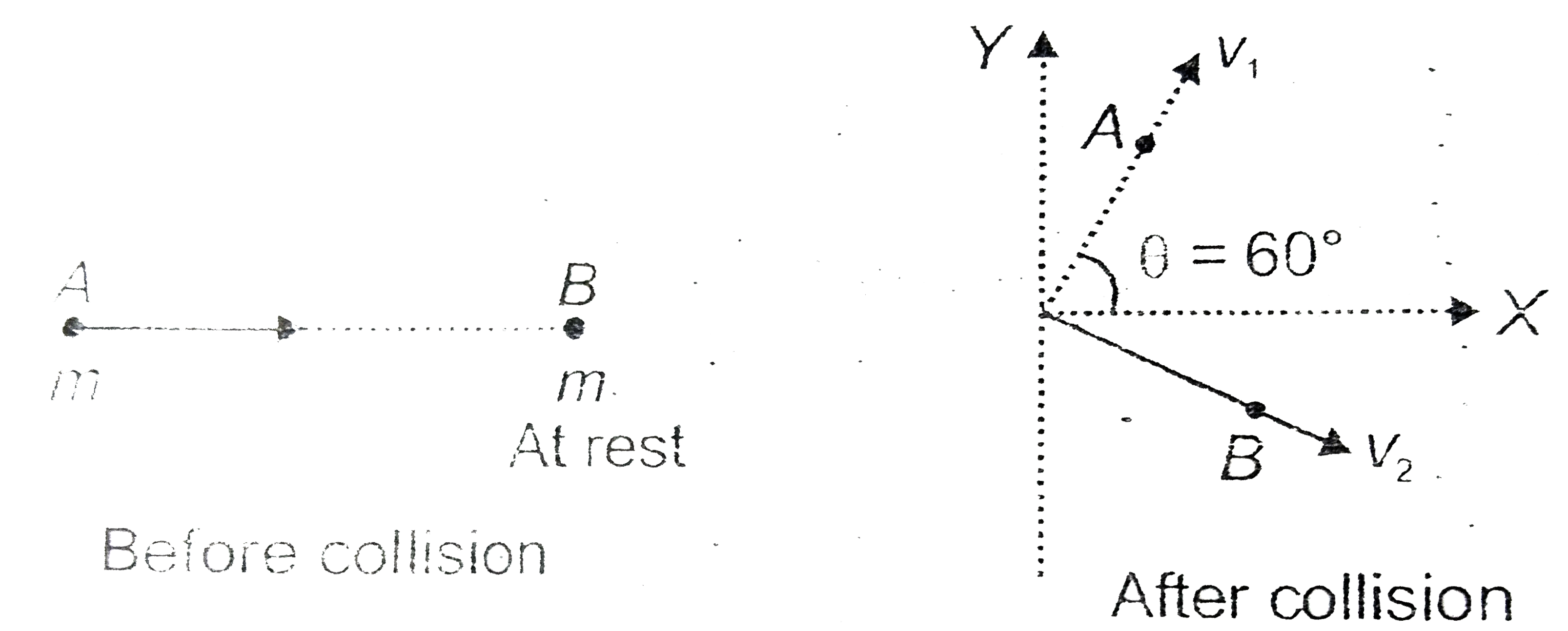
A & B have same mass and the collision is perfectly elastic
∴θ+ϕ=90∘
ϕ=90∘−60∘=30∘ …(i)
Using law of conservation of linear momentum
(a) For X-components
u=5=v(1)cos60∘+v2cos30∘
5=v12+v2√32
10=v1+v2√3 ...(ii)
(b) For Y-components
0=v1sin60∘−v2sin30∘
v1√32=v22
v1√3=v2 ...(iii)
From equations (ii) & (iii)
10=v1+3v1
v1=2.5ms−1
v2=v1√3==2.5×1:732
v2=4.33ms−1
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A and B are two particles having the same mass m. A is moving along X-axis with a speed of 10ms−1 and B is at rest. After undergoing a perfectly elastic collision with B, particle A gets scattered through an angle of 30∘. What is th edirection of motion of B, and the speeds of A and B, after the collision?
View SolutionTwo particles each of mass m moving with equal speed 2m/s along the indicated direction in the figure undergo a perfectly inelastic collision.Velocity of combined system after collision is ?
View Solution
Knowledge Check
Particle A makes a perfectly elastic collision with another particle B at rest. They fly apart in opposite directions with equal speeds. The ratio of their masses mA/mB is
A12B13C14D1√3Particle A makes a perfectly elastic collision with anther particle B at rest. They fly apart in opposite direction with equal speeds. If the masses are mA&mB respectively, then
A2mA=mBB3mA=mBC4mA=mBD√3mA=mBA marble going at a speed of 2ms−1 hits another marble of equal mass at rest. If the collision is perfectly elastic, then the velocity of the first marble after collision is
A4ms−1B0ms−1C2ms−1D3ms−1
Two particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
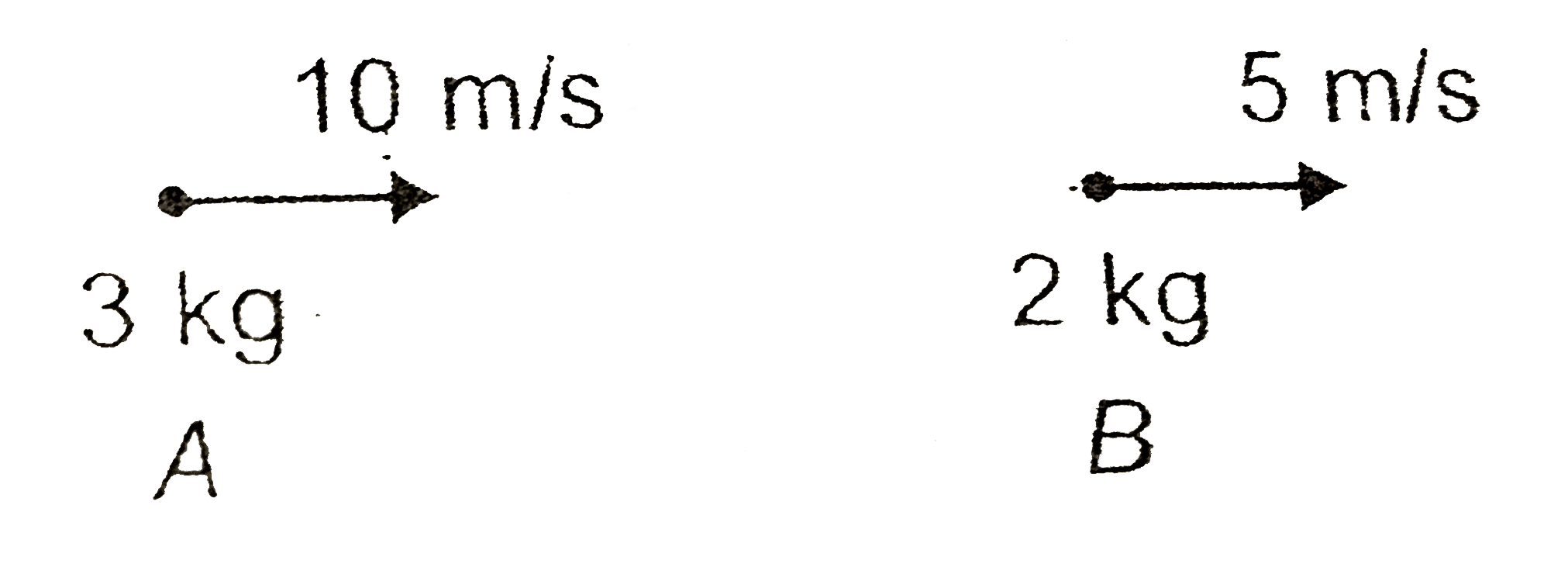
Find the maximum momentum that particle B can have after collision with B.
View SolutionA and B are two identical balls. A moving with a speed of 6m/s, along the positive X-axis, undergoes a collision with B initially at rest. After collision, each ball moves along directions making angles of ±30∘ with the X-axis. What are the speeds of A and B after the collision ? I s this collision perfectly eleastic ?
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
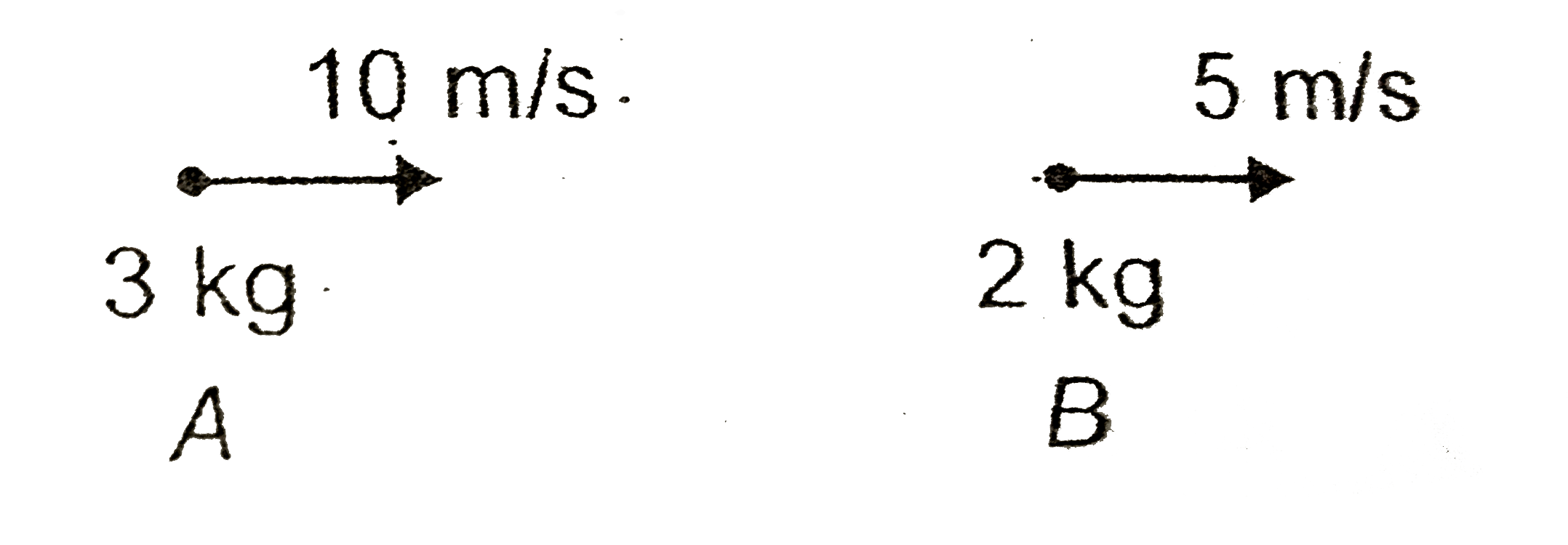
Find the maximum momentum that particles A can have after collision with B.
View SolutionA neutron moving at a speed v undergoes a head-on elastic collision with a nucleus of mass number A at rest. The ratio of the kinetic energies of the neutron after and before collision is :
View SolutionTwo identical balls moving in opposite directions with speed 20 m/s and 25 m/s undergo head on perfectly inelastic collision. The speed of combined mass after collision is
View Solution