Consider objects of masses m1andm2 moving initially along the same straight line with velocities u1andu2 respectively. Considering a perfectly elastic collision (with u1>u2) derive expressions for their velocities after collision.
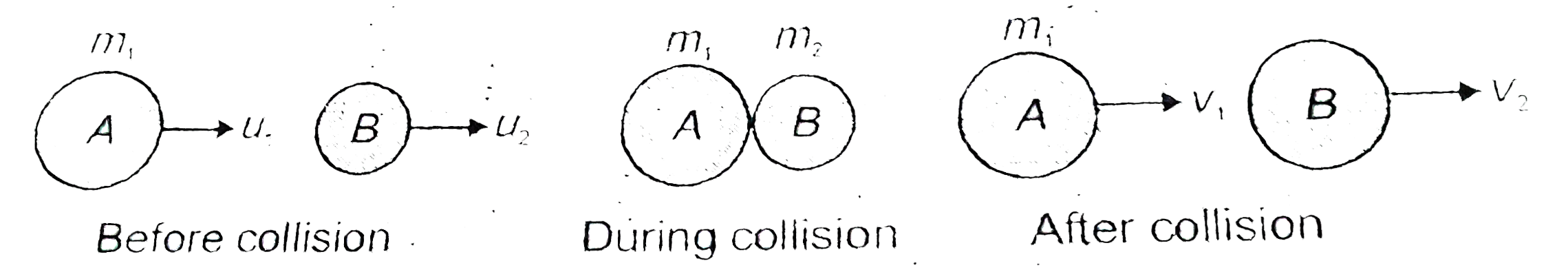
With u1>u2
Relative velocity of approach before collision =u1−u2 …(i)
Let the veocity of A after collision be v1 and the velocity of B after collision be v2.
When v2>v1, teh bodies separate after collision.
Relative velocity of spearafion after collision =v2−v1 ...(i)
Linear momentum of the two balls before colision =v2−v1 ...(ii)
Linear momentum of the two balls before collision =m1r1+m2u2
Linear momentum of hte two balls after colision =m1v1+m2v2
m1v1+m2v2=m1u1+m2u2 ...(iii)
According to the law of conservation of linear momentum
or m2(v2−u2)=m1(u1−v1) ...(iv)
Total KE of the two balls before collision =12m1u21+12m2u22 ...(v)
Total KE of the two balls after collision
=12m1v21+12m2v22 ...(vi)
12m1v21+12m2v22=12+12m2u22 According to the law of conservation of KE 12m2(v22−u22)=12(u21−y21)
or m2(v22−u22)=m1(u21−v21) ...(vii)
Dividing equation (vii) by equation (iv),
m2(v22−u22)m2(v2−u2)=m1(u21−v21)m1(u1−v1)
(v2+u2)(v2−u2)(v2−u2)=(u1+v1)(u1−v1)(u1−v1)
or v2+u2=u1+v1
or v2−v1=u1−u2 ...(viii)
Hence in one-dimensional elastic collision (from equationa (i) & (ii))
From equation (viii) , v2−v1u1−u2=1
By definition, v2−v1u1−u2=0=1
Hence, coefficient fo restitution/resilience of a perfectly elastic collision in one dimension is unity From equation (viii), ...(ix)
v2=u1−u2+v1
Put this value in equation (iii)
m1v1+m2(u1−u2+v1)=m1u1+m2u2
m1v1+m2u1−m2u2+m2v1=m1u1+m2u2
v1(m1+m2)=(m1−m2)u1+2m2u2
v1=(m1−m2)u1(m1+m2)+2m2u2m1+m2 ...(x)
Put this value of v1 fro equation (x) in equation (ix)
v2=u1−u2+(m1−m2)u1m1+m2+2m2u2m1+m2
=u1[1+m1−m2m1+m12]+u2[2m2m1+m2−1]
=u1[m1+m2+m1−m2m1+m2]+u2[2m2−m1−m2m1+m2]
v2=2m1u1m1+m2+(m2−m1)u2(m1+m2) ...(xi)
Note: You can get exp. for v2 from equation (x) by interchanging m1andm2andu1andu2You can also get equation (x) from equation (xi).
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
Derive final velocities V1andV2 after perfectly elastic collision.
View SolutionTwo spheres made of clay of masses 'm1' and 'm2' moving along a straight line in the same direction collide with each other. Their velocities just before collision are 'u1' and 'u2' respectively. After collision, they stick together and move with teh same velocity, in the same direction, along the straight line. Find the velocity with which they move together.
View Solution
Knowledge Check
Two equal masses m1 and m2 moving along the same straight line with velocites +3m/s and −5m/s respectively collide elastically. Their velocities after the collision will be respectively.
A+4m/s for bothB−3m/sand+5m/sC−4m/sand+4m/sD−5m/sand+3m/sTwo particles of same mass m moving with velocities u1 and u2 collide perfectly inelastically. The loss of energy would be :
A1/2m(u1−u2)2B1/4m(u1−u2)2Cm(u1−u2)2D2m(u1−u2)2Two identical mass M moving with velocity u1andu2 collide perfectly inelastically. The loss in kinetic energy is
AM2(u2−u1)2BM2(u21−u22)CM4(u2−u1)2DM4(u21−u22)
Two spheres made of clay of masses 'm1' and 'm2' moving along a straight line in the same direction collide with each other. Their velocities just before collision are 'u1' and 'u2' respectively. After collision, they stick together and move with teh same velocity, in the same direction, along the straight line. Find the velocity with which they move together.
View SolutionConsider on object of mass m moving with velocity v0 and all other masses at rest initially. Find the % loss in energy after final collision. If all collision are perfectly inelastic.

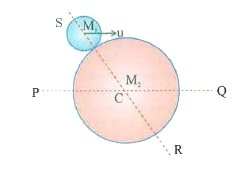
View SolutionAn object of mass M1 moving horizontally with speed u collides elastically with another object of mass M2 at rest. Select correct statement.
View SolutionTwo perfectly elastic particles A and B of equal masses travelling along a line joining them with velocities 15m/s and 10m/s respectively collide. Their velocities after the elastic collision will be (in m/s) respectively
View SolutionTwo particles of masses m1 and m2 and velocities u1 and αu1(α≠0) make an elastic head on collision. If the initial kinetic energies of the two particles are equal and m1 comes to rest after collision, then
View Solution
