A stone is thrwon vertically upwards. On its way is passes point A with a speed v and passes point B, 30 m higher than A with speed $\frac{v}{2}$ . Find (i) The speed v (ii) The maximum height reached by the stone above point B.

Video Solution

Text Solution

Verified by Experts

Let us choose the positive direction along vertically upward.
(i) Between the point A and B, using equation $v^{2} = u^{2} + 2 a s$ , we get
${(+ \frac{v}{2})}^{2} = {(+ v)}^{2} + 2 (- g) (+ 30)$
$\frac{v^{2}}{4} = v^{2} - 60 g$
along the $60 g = v^{2} - \frac{v^{2}}{4} = \frac{3}{4} v^{2}$

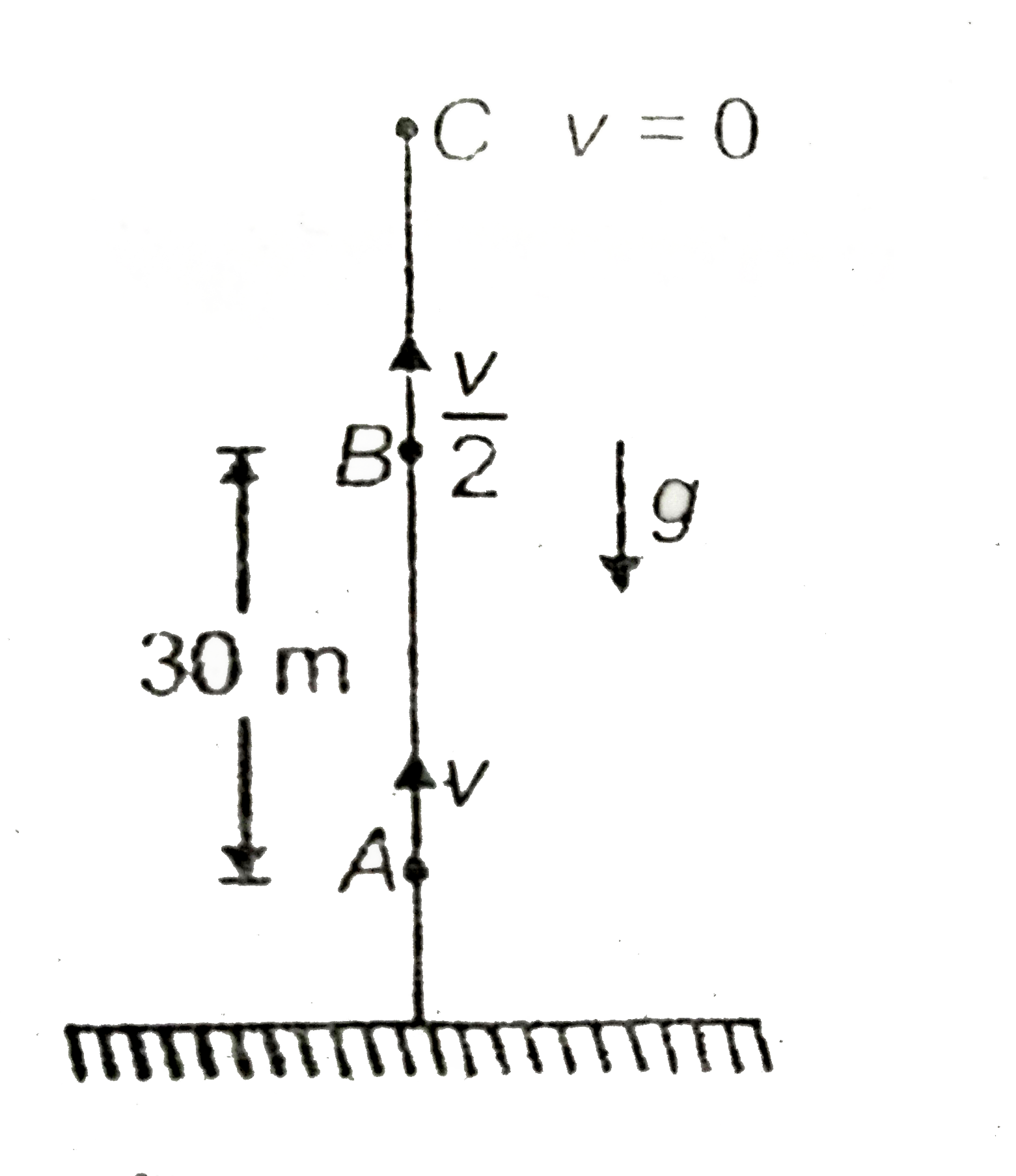
$\frac{3}{4} v^{2} = 60 g$
$\Rightarrow v^{2} = 60 \times \frac{4}{3} \times g$
$v^{2} = 80 \times 9.8 = 8 \times 98$
$v^{2} = 4 \times 2 \times 2 \times 49$
$v = \sqrt{4 \times 2 \times 2 \times 49} = 2 \times 2 \times 7 = 28 m / s$
(ii) The speed at $B = \frac{v}{2} = \frac{28}{2} = 14 m / s$
Again using the equation, $v^{2} = u^{2} + 2 a s$ between B and C
$0 = {(+ \frac{v}{2})}^{2} + 2 (- g) (+ s)$
$2 g s = {(14)}^{2} = 14 \times 14$
$s = \frac{14 \times 14}{2 \times 9.8} = \frac{14 \times 14 \times 10}{2 \times 2 \times 49} = \frac{40}{4} = 10 m$
The maximum height attained above B is 10 m.

Updated on:21/07/2023

A stone is thrown vertically upwards with an initial speed $u$ from the top of a tower, reaches the ground with a speed $3 u$ . The height of the tower is :
A $\frac{3 u^{2}}{g}$
B $\frac{4 u^{2}}{g}$
C $\frac{6 u^{2}}{g}$
D $\frac{9 u^{2}}{g}$
A stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is $10 m s^{- 1}$ , then the maximum height attained by the stone is ( $g = 10 m s^{- 2}$ )
A25 m
B10 m
C15 m
D20 m