Starting with the thermodynamic relationship , ,derive the following relationship
To derive the relationship ΔG=−TΔStotal from the thermodynamic relationship G=H−TS, we can follow these steps:
Step 1: Start with the Gibbs Free Energy Equation
The Gibbs free energy G is defined as:
G=H−TS
Step 2: Differentiate the Gibbs Free Energy
To find the change in Gibbs free energy (ΔG), we differentiate the equation:
ΔG=ΔH−TΔS−SΔT
However, for constant temperature, the term SΔT becomes zero, simplifying our equation to:
ΔG=ΔH−TΔS
Step 3: Express ΔS in terms of the system and surroundings
The total entropy change of the universe is given by:
ΔStotal=ΔSsystem+ΔSsurroundings
For the surroundings, we can express ΔSsurroundings as:
ΔSsurroundings=−ΔHsystemT
This is because the heat lost or gained by the system is equal and opposite to that of the surroundings.
Step 4: Substitute ΔSsurroundings into the total entropy equation
Substituting this into the total entropy change gives:
ΔStotal=ΔSsystem−ΔHsystemT
Step 5: Rearranging the equation
Rearranging the above equation, we find:
TΔStotal=TΔSsystem−ΔHsystem
Step 6: Substitute back into the Gibbs Free Energy equation
Now, we can substitute this expression back into the equation for ΔG:
ΔG=ΔH−TΔSsystem
Using the rearranged equation:
ΔG=−TΔStotal
Conclusion
Thus, we have derived the desired relationship:
ΔG=−TΔStotal
---
The Gibbs free energy G is defined as:
G=H−TS
To find the change in Gibbs free energy (ΔG), we differentiate the equation:
ΔG=ΔH−TΔS−SΔT
However, for constant temperature, the term SΔT becomes zero, simplifying our equation to:
ΔG=ΔH−TΔS
The total entropy change of the universe is given by:
ΔStotal=ΔSsystem+ΔSsurroundings
For the surroundings, we can express ΔSsurroundings as:
ΔSsurroundings=−ΔHsystemT
This is because the heat lost or gained by the system is equal and opposite to that of the surroundings.
Substituting this into the total entropy change gives:
ΔStotal=ΔSsystem−ΔHsystemT
Rearranging the above equation, we find:
TΔStotal=TΔSsystem−ΔHsystem
Now, we can substitute this expression back into the equation for ΔG:
ΔG=ΔH−TΔSsystem
Using the rearranged equation:
ΔG=−TΔStotal
Thus, we have derived the desired relationship:
ΔG=−TΔStotal
Topper's Solved these Questions
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:COMPETITION FOCUS (JEE ( main andAdvanced ) /Medical Entrance Special)
Explore 131 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Comprehension 1
Explore 1 Video
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:ADDITIONAL QUESTIONS(VERY SHORT ANSWER QUESTIONS)
Explore 43 Videos
- STRUCTURE OF ATOMBook:PRADEEPChapter:STRUCTURE OF ATOMExercise:Competition Focus (JEE (Main and Advanced)/Medical Entrance (IX. Assertion And Reason Type Questions (Type II))
Explore 12 Videos
Similar Questions
Knowledge Check
Which of the following relationship is true?
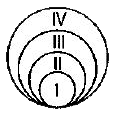 AI-Whole Numbers, II-Natural Numbers, III-Integers, IV-Rational NumbersBI-Rational Nurnbers, II-Integers, III-Whole Numbers, IV-Natual NumbersCI-Natural Numbers, II-Whole Numbers,
AI-Whole Numbers, II-Natural Numbers, III-Integers, IV-Rational NumbersBI-Rational Nurnbers, II-Integers, III-Whole Numbers, IV-Natual NumbersCI-Natural Numbers, II-Whole Numbers,
III-Integers, IV-Rational NumbersDNone of the aboveWhich of the following relationships is true?
AMolecular mass =(Vapor density of gas)2BMolecular mass =12 (Vapor densiy of gas)CMolecular mass =2×(Vapor density of gas)DMolecular mass =√Vapor density of gasWhich of the following relationship are correct?
AΔH−ΔEΔn×T=ConstantBΔG=−TΔSTotalCK=e−ΔG∘/RTD[∂(ΔH)∂T]P=ΔCp
Which of the following relationship is correct ?
View SolutionWhat is relationship between the following projections?

View SolutionWhich of the following relationships are wrong?
View SolutionWhich one of the following relationship is correct?
View SolutionWhich of the following relationships is not correct ?
View Solution
