Specific heat of an elementary gas is found to be 0.313 J at constant volume. If the molar mass of the gas is 40 g mol−1 , what is the atomicity of the gas ?
The correct Answer is:monoatomic
To determine the atomicity of the gas given its specific heat at constant volume (Cv) and molar mass, we can follow these steps:
Step 1: Identify the given values
- Specific heat at constant volume (Cv) = 0.313 J/g·K
- Molar mass of the gas (M) = 40 g/mol
Step 2: Calculate Cv in terms of J/mol·K
To convert the specific heat from J/g·K to J/mol·K, we use the formula:
Cv=Sv×M
Where:
- Sv = specific heat at constant volume (0.313 J/g·K)
- M = molar mass (40 g/mol)
Calculating:
Cv=0.313J/g⋅K×40g/mol=12.52J/mol⋅K
Step 3: Calculate Cp using the relation Cp = Cv + R
The relation between the specific heats at constant pressure and constant volume is given by:
Cp=Cv+R
Where:
- R = universal gas constant = 8.314 J/mol·K
Calculating:
Cp=12.52J/mol⋅K+8.314J/mol⋅K=20.834J/mol⋅K
Step 4: Calculate the ratio of Cp to Cv (γ)
The ratio of specific heats (γ) is given by:
γ=CpCv
Calculating:
γ=20.834J/mol⋅K12.52J/mol⋅K≈1.666
Step 5: Relate γ to atomicity (F)
For an ideal gas, the relationship between γ and the degrees of freedom (F) is given by:
γ=1+2F
Rearranging this equation to find F:
γ−1=2F
F=2γ−1
Substituting the value of γ:
F=21.666−1=20.666≈3
Step 6: Determine the atomicity of the gas
The degrees of freedom (F) for a monoatomic gas is 3, which indicates that the gas is monoatomic.
Final Answer
The atomicity of the gas is 1 (indicating it is a monoatomic gas).
---
- Specific heat at constant volume (Cv) = 0.313 J/g·K
- Molar mass of the gas (M) = 40 g/mol
To convert the specific heat from J/g·K to J/mol·K, we use the formula:
Cv=Sv×M
Where:
- Sv = specific heat at constant volume (0.313 J/g·K)
- M = molar mass (40 g/mol)
Cv=0.313J/g⋅K×40g/mol=12.52J/mol⋅K
The relation between the specific heats at constant pressure and constant volume is given by:
Cp=Cv+R
Where:
- R = universal gas constant = 8.314 J/mol·K
Cp=12.52J/mol⋅K+8.314J/mol⋅K=20.834J/mol⋅K
The ratio of specific heats (γ) is given by:
γ=CpCv
γ=20.834J/mol⋅K12.52J/mol⋅K≈1.666
For an ideal gas, the relationship between γ and the degrees of freedom (F) is given by:
γ=1+2F
γ−1=2F
F=2γ−1
F=21.666−1=20.666≈3
The degrees of freedom (F) for a monoatomic gas is 3, which indicates that the gas is monoatomic.
The atomicity of the gas is 1 (indicating it is a monoatomic gas).
Topper's Solved these Questions
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - PROBLEM FOR PRACTICE
79 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - CURIOSITY QUESTIONS
4 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - 33390
1 Videos
- STRUCTURE OF ATOMBOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Competition Focus (JEE (Main and Advanced)/Medical Entrance (IX. Assertion And Reason Type Questions (Type II))
12 Videos
Similar Questions
Molar heat capacity of a gas at constant volume.
View SolutionThe molar specific heats of an ideal gas at constant volume and constant pressure are respectively 4.98 and 6.96 cal mol−1K−1. If the molecular weight of the gas be 32, then calculate the root means square speed of the molecule of the gas at 120∘C. (1 cal = 4.2 J)
View Solution
Knowledge Check
The specific heat of gas is found to be 0.075 calories at constant volume and its formula weight is 40. The atomicity of the gas would be
AOneBTwoCThreeDFourMolar specific heat at constant volume Cv for a monatomic gas is
A32RB52RC3RD2RGraph for specific heat at constant volume for a monoatomic gas
A B
B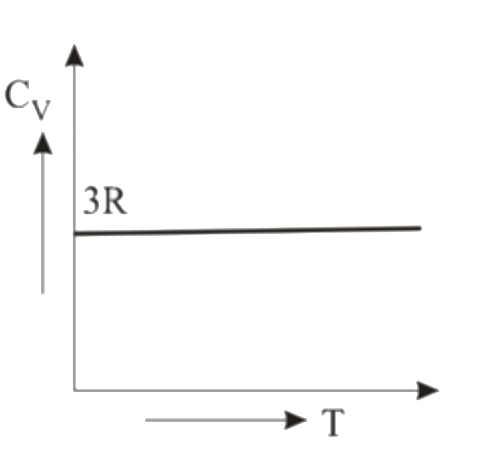 C
C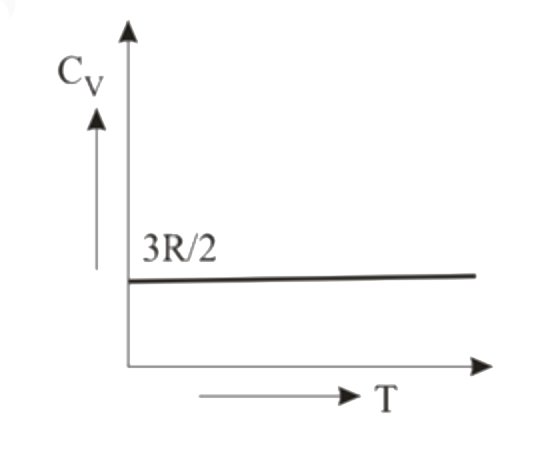 D
D
The specific heats of an ideal gas at constant volume and constant pressure are respectively 4.98 and 6.96 cal mol−1K−1. If the molecular weight of the gas be 32, then calculate the root-mean square speed of the molecules of the gas at 120∘C, (1 cal=4.2J)
View SolutionThe specific heat of a monoatomic gas at constant pressure is 248.2 J kg−1K−1 and at constant volume it is 149.0 J kg−1K−1. Find the mean molar mass of the gas.
View SolutionIf the molar specific heat of a gas at constant pressure is 72R, then the atomicity of gas is
View SolutionGraph for specific heat at constant volume for a monoatomic gas
View SolutionThe molar specific heat at constant volume, for a non linear triatomic gas is
View Solution
