A heated copper block at 130∘C loses 340 J of heat to the surroundings which are at room temperature of 32∘C . Calculate
(i) the entropy change of the system ( copper block ) (ii) the entropy change in the surrounding
(iii) the total entropy change in the universe due to this process
Assume that the temperature of the block and the surroundings remains constant.
To solve the problem, we will calculate the entropy changes step by step.
Given Data:
- Temperature of the copper block, Tblock=130∘C=130+273.15=403.15K
- Temperature of the surroundings, Tsurroundings=32∘C=32+273.15=305.15K
- Heat lost by the copper block, Q=340J
Step 1: Calculate the Entropy Change of the System (Copper Block)
The entropy change of the system can be calculated using the formula:
ΔSsystem=−QTblock
Substituting the values:
ΔSsystem=−340J403.15K
Calculating this gives:
ΔSsystem≈−0.843J/K
Step 2: Calculate the Entropy Change of the Surroundings
The entropy change of the surroundings can be calculated using the formula:
ΔSsurroundings=QTsurroundings
Substituting the values:
ΔSsurroundings=340J305.15K
Calculating this gives:
ΔSsurroundings≈1.113J/K
Step 3: Calculate the Total Entropy Change in the Universe
The total entropy change in the universe is the sum of the entropy changes of the system and the surroundings:
ΔSuniverse=ΔSsystem+ΔSsurroundings
Substituting the values:
ΔSuniverse=−0.843J/K+1.113J/K
Calculating this gives:
ΔSuniverse≈0.270J/K
Summary of Results:
(i) The entropy change of the system (copper block) is approximately −0.843J/K.
(ii) The entropy change of the surroundings is approximately 1.113J/K.
(iii) The total entropy change in the universe is approximately 0.270J/K.
- Temperature of the copper block, Tblock=130∘C=130+273.15=403.15K
- Temperature of the surroundings, Tsurroundings=32∘C=32+273.15=305.15K
- Heat lost by the copper block, Q=340J
ΔSsystem=−QTblock
Substituting the values:
ΔSsystem=−340J403.15K
Calculating this gives:
ΔSsystem≈−0.843J/K
ΔSsurroundings=QTsurroundings
Substituting the values:
ΔSsurroundings=340J305.15K
Calculating this gives:
ΔSsurroundings≈1.113J/K
ΔSuniverse=ΔSsystem+ΔSsurroundings
Substituting the values:
ΔSuniverse=−0.843J/K+1.113J/K
Calculating this gives:
ΔSuniverse≈0.270J/K
(i) The entropy change of the system (copper block) is approximately −0.843J/K.
(ii) The entropy change of the surroundings is approximately 1.113J/K.
(iii) The total entropy change in the universe is approximately 0.270J/K.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Problem 4
2 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Problem 5
1 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Problem 2
4 Videos
- STRUCTURE OF ATOMBOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Competition Focus (JEE (Main and Advanced)/Medical Entrance (IX. Assertion And Reason Type Questions (Type II))
12 Videos
Similar Questions
A heated copper block at 130∘C loses 340 J of heat to the surroundings, which are at room temperature of 32∘C. Calculate total entropy change in the universe due to this process.
View SolutionA heated irron block at 127∘C loses 300J of heat to the surroundings which are at a temperature of 27∘C. This process is 0.05JK−1. Find the value of x.
View Solution
Knowledge Check
Some entropy change are represented in fig. Select correct entropy change:
 AΔS1,ΔS2,ΔS3BΔS1,ΔS2,ΔS4CΔS1,ΔS2,ΔS3,ΔS4DΔS2andΔS4
AΔS1,ΔS2,ΔS3BΔS1,ΔS2,ΔS4CΔS1,ΔS2,ΔS3,ΔS4DΔS2andΔS4In a spontaneous irreversible process the total entropy of the system and surroundings
AEquals zeroBDecreasesCIncreasesDRemains constantSome entropy change are represented infigure. Select correct entropy change.
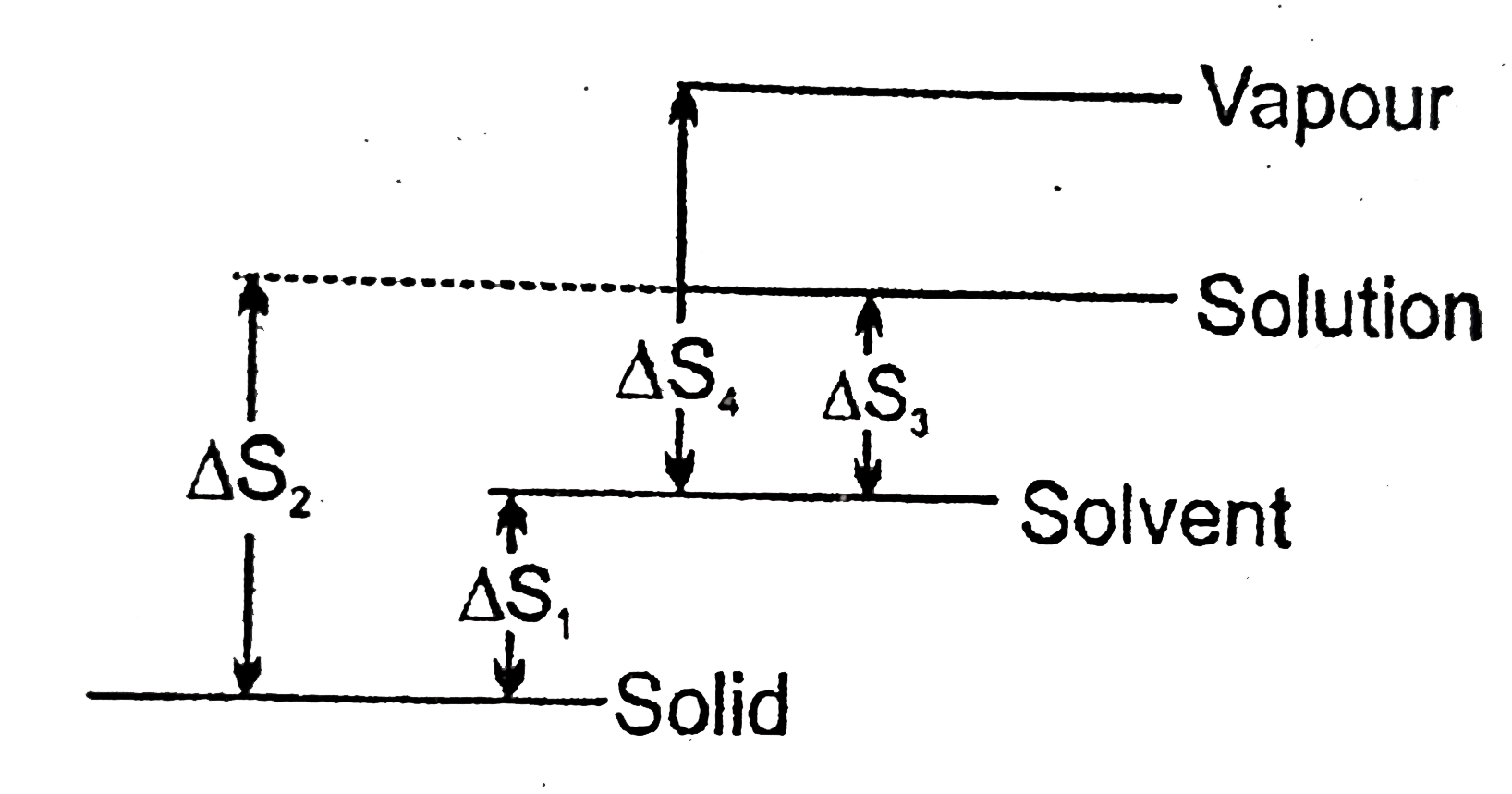 AΔS1,ΔS2,ΔS3BΔS1,ΔS2,ΔS4CΔS1,ΔS2,Δ3,ΔS4DΔS2 and ΔS4
AΔS1,ΔS2,ΔS3BΔS1,ΔS2,ΔS4CΔS1,ΔS2,Δ3,ΔS4DΔS2 and ΔS4
Entropy Change for System and surrounding
View SolutionA heated iron block at 127 ∘C loses "300J of heat to the surrounding which is at a temperature of 27∘C.Delta S for this process is 0.05xJK^(-1) Find the value of x.
View Solution10 kg of cold water at 2∘C absorbs 50J of heat from the surrounding which were at a temperature of37∘C . What is the entropy change of (i) the system (ii) the surroundings (iii) the universe ? Assume the change in temperature of the water and the surroundings to be negligible.
View SolutionFor a process, entropy change of a system is expressed as
View SolutionEntropy change for an adiabatic reversible process is
View Solution
