2×108 atoms of carbon are arranged side by side. Calculate the radius of carbon atom if the length of this arrangement is 3.0 cm
To solve the problem of calculating the radius of a carbon atom when 2x108 atoms are arranged side by side in a length of 3.0cm, we can follow these steps:
Step 1: Understand the relationship between length, number of atoms, and radius
The total length of the arrangement is equal to the number of atoms multiplied by the diameter of one atom.
Step 2: Write the formula
Let r be the radius of a carbon atom. The diameter d of a carbon atom is given by:
d=2r
The total length L can be expressed as:
L=N×d
where N is the total number of atoms.
Step 3: Substitute known values
From the problem, we know:
- Total length L=3.0cm=3.0×10−2m
- Total number of carbon atoms N=2×108
Substituting these values into the formula gives:
3.0×10−2=(2×108)×(2r)
Step 4: Solve for the radius
Rearranging the equation to solve for r:
3.0×10−2=4×108×r
r=3.0×10−24×108
Calculating r:
r=3.04×10−2×10−8
r=0.75×10−10m
r=7.5×10−11m
Step 5: Convert radius to nanometers
To convert meters to nanometers, we use the conversion factor 1nm=10−9m:
r=7.5×10−11m=0.075nm
Final Answer
The radius of a carbon atom is 0.075nm.
---
The total length of the arrangement is equal to the number of atoms multiplied by the diameter of one atom.
Let r be the radius of a carbon atom. The diameter d of a carbon atom is given by:
d=2r
The total length L can be expressed as:
L=N×d
where N is the total number of atoms.
From the problem, we know:
- Total length L=3.0cm=3.0×10−2m
- Total number of carbon atoms N=2×108
3.0×10−2=(2×108)×(2r)
Rearranging the equation to solve for r:
3.0×10−2=4×108×r
r=3.0×10−24×108
r=3.04×10−2×10−8
r=0.75×10−10m
r=7.5×10−11m
To convert meters to nanometers, we use the conversion factor 1nm=10−9m:
r=7.5×10−11m=0.075nm
The radius of a carbon atom is 0.075nm.
Topper's Solved these Questions
- STRUCTURE OF ATOMBook:PRADEEPChapter:STRUCTURE OF ATOMExercise:NCERT Exemplar Problems With Answers, Hints and Solution (I. Multiple Choice Questions)
Explore 16 Videos
- STRUCTURE OF ATOMBook:PRADEEPChapter:STRUCTURE OF ATOMExercise:NCERT Exemplar Problems With Answers, Hints and Solution (II. Multiple Choice Questions)
Explore 5 Videos
- STRUCTURE OF ATOMBook:PRADEEPChapter:STRUCTURE OF ATOMExercise:Conceptual Questions
Explore 44 Videos
- STATES OF MATTER: SOLID MATTERBook:PRADEEPChapter:STATES OF MATTER: SOLID MATTERExercise:COMPETITION FOCUS (ASSERTION-REASON)
Explore 17 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:MULTIPLE CHOICE QUESTION ( BASED ON PRACTICAL CHEMISTRY)
Explore 3 Videos
Similar Questions
Knowledge Check
The correct relation for radius of atom and edge - length in case of fcc arrangement is
Ar=a2Br=√3a4Cr=a2√2Dr=4a√3The bond length between hybridised carbon atom and other carbon atom is minimum in
ApropeneBpropyneCpropaneDbutaneArrange the following atoms in the ascending order of atomic radius
AF,Cl,O,CBC,O,F,ClCO,C,F,ClDF,O,C,Cl
Calculate the total number of chiral carbon atoms in.
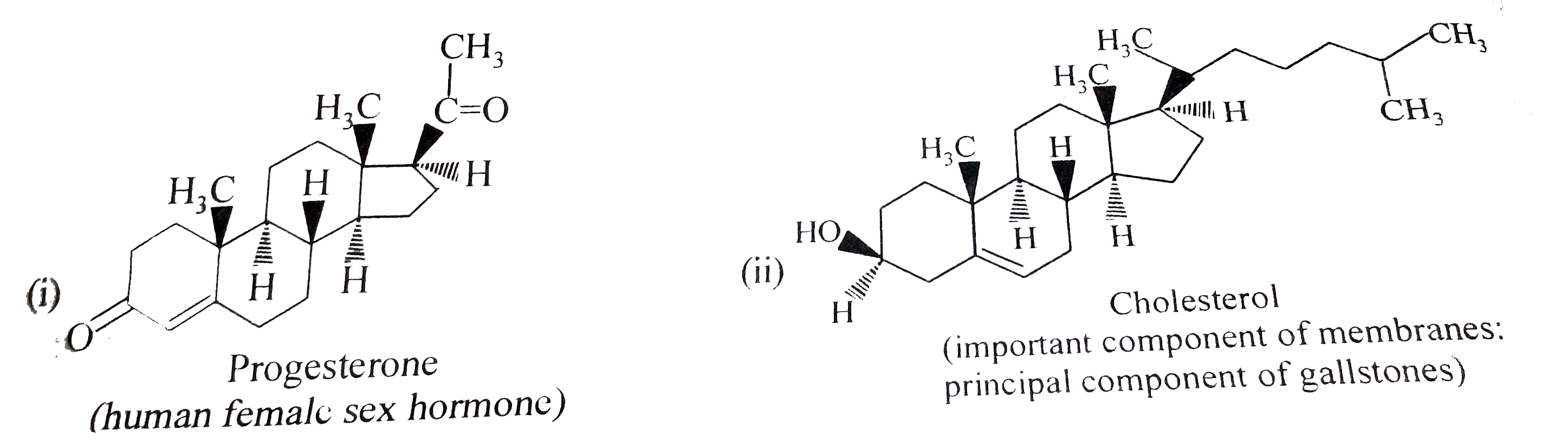
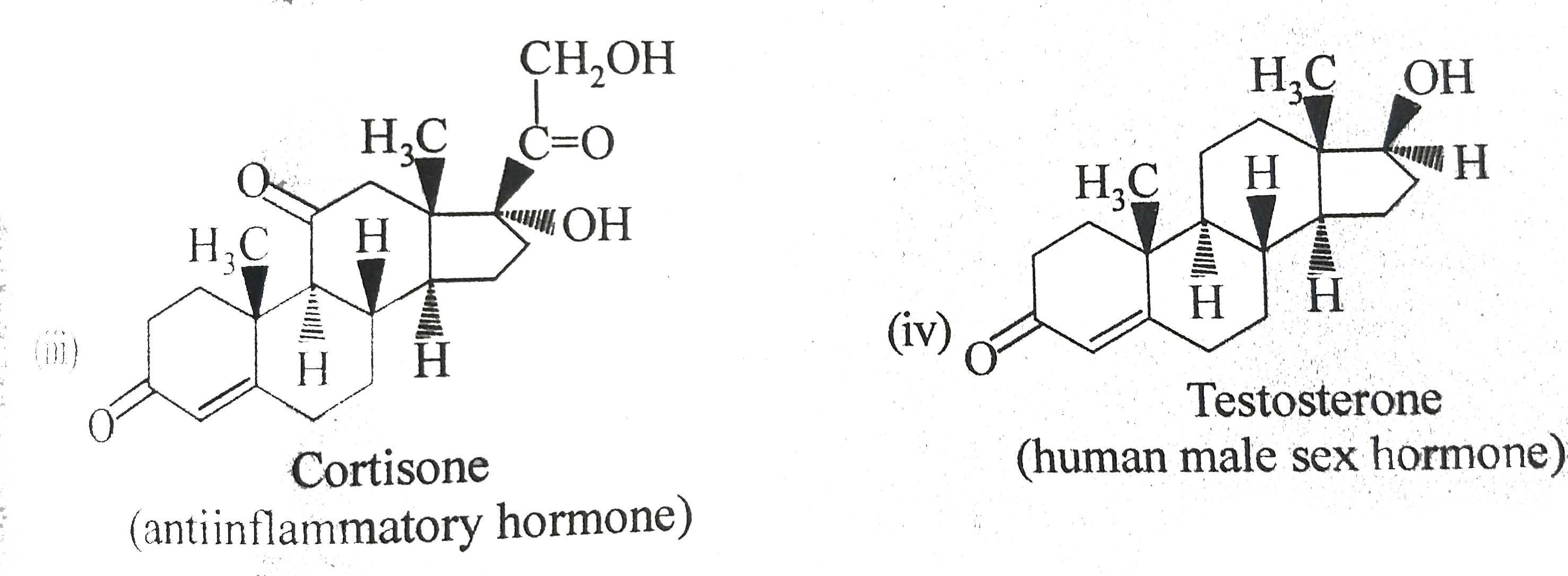
View SolutionIn which form are the carbon atoms in graphite arranged?
View SolutionThe ratio of masses of carbon and oxygen is 3 : 8 and their atomic masses are 12 and 16 respectively in a molecule of carbon dioxide. Calculate the ratio of atoms of carbon and oxygen in the molecule of carbon dioxide.
View SolutionIf the diameter of a carbon atom is 0.15nm, calculate the number of carbon atom which can be placed side by side in a straight line length of scale of length 20cm long.
View SolutionCarbon atom in diamond are arranged in
View Solution