What are tetrahedral and octahdral voids ? How are their radii related to the radii of the spheres in the close packed arrangement ?
Step-by-Step Solution
1. Definition of Tetrahedral and Octahedral Voids:
- Tetrahedral Voids: These are the spaces formed in a close-packed arrangement of spheres where four spheres are positioned at the corners of a tetrahedron. In a crystal lattice, when you have a close-packed structure, the tetrahedral voids are created when one sphere is placed above the triangular base formed by three spheres.
- Octahedral Voids: These voids are formed when six spheres are arranged in such a way that they form the corners of an octahedron. In a close-packed structure, an octahedral void is created when one sphere is placed at the center of the octahedron formed by the surrounding six spheres.
2. Arrangement of Spheres:
- In a close-packed arrangement, spheres are tightly packed to maximize the space they occupy. For tetrahedral voids, there are typically two tetrahedral voids for every unit cell in a face-centered cubic (FCC) structure. For octahedral voids, there is one octahedral void at the center of the unit cell and one at the edge of the unit cell.
3. Relationship of Radii:
- The radius of the tetrahedral void (r_t) in relation to the radius of the spheres (R) in a close-packed arrangement is given by:
rt=0.225R(minimum radius)andrt=0.414R(maximum radius)
- The radius of the octahedral void (r_o) is given by:
ro=0.414R(minimum radius)andro=0.732R(maximum radius)
4. Conclusion:
- In summary, tetrahedral and octahedral voids are important concepts in solid-state chemistry, particularly in the study of crystal structures. The radii of these voids are directly related to the radii of the spheres in a close-packed arrangement, with specific ratios that define their sizes.
- Tetrahedral Voids: These are the spaces formed in a close-packed arrangement of spheres where four spheres are positioned at the corners of a tetrahedron. In a crystal lattice, when you have a close-packed structure, the tetrahedral voids are created when one sphere is placed above the triangular base formed by three spheres.
- Octahedral Voids: These voids are formed when six spheres are arranged in such a way that they form the corners of an octahedron. In a close-packed structure, an octahedral void is created when one sphere is placed at the center of the octahedron formed by the surrounding six spheres.
- In a close-packed arrangement, spheres are tightly packed to maximize the space they occupy. For tetrahedral voids, there are typically two tetrahedral voids for every unit cell in a face-centered cubic (FCC) structure. For octahedral voids, there is one octahedral void at the center of the unit cell and one at the edge of the unit cell.
- The radius of the tetrahedral void (r_t) in relation to the radius of the spheres (R) in a close-packed arrangement is given by:
rt=0.225R(minimum radius)andrt=0.414R(maximum radius)
- The radius of the octahedral void (r_o) is given by:
ro=0.414R(minimum radius)andro=0.732R(maximum radius)
- In summary, tetrahedral and octahedral voids are important concepts in solid-state chemistry, particularly in the study of crystal structures. The radii of these voids are directly related to the radii of the spheres in a close-packed arrangement, with specific ratios that define their sizes.
Topper's Solved these Questions
- APPENDIXBook:PRADEEPChapter:APPENDIXExercise:6 WHAT HAPPENS WHEN
Explore 1 Video
- APPENDIXBook:PRADEEPChapter:APPENDIXExercise:7 WHAT HAPPENS WHEN
Explore 1 Video
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBook:PRADEEPChapter:CHEMICAL BONDING AND MOLECULAR STRUCTUREExercise:Curiosity Questions
Explore 2 Videos
Similar Questions
How many tetrahedral and octahedral void spaces are there for each sphere in close packing?
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View Solution
Knowledge Check
If in a closest packed arrangement r is the radius of the sphere respresenting the tetrahedral void and R is the radius of the spheres in closest packed arrangement then
Ar/R=0.732Br/R=0.155Cr/R=0.225Dr/R=0.414Which of the following statement is correct for a closet packed structure? (i) Each tetrahedral void is surrounded by 4 spheres and each sphere is surrounded by 8 tetrahedral voids.
(ii) Each octahedral voids is surrounded by 6 spherus and each sphere is surrounded by 6 octahedral voids.
(iii) The number of tetrahedral voids in a closest-packed arrangement is twice the number of spheres.
(iv) The number of octahedral voids in a closest-packed arrangement is equal to the number of spheres.A(i), (ii)B(iii), (iv)C(i), (iii)D(i), (ii), (iii), (iv)The arrangement of spheres in hexagonal close packing (hcp) is :
AABC ABC......'BAAA BBB.CAB'ABDAA BC ......
In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
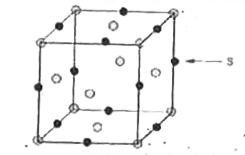
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defect
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the spinel structure, oxide ions are cubic close packed whereas 1/8th of tetrahedral voids are occupied by A2+ cations and 1/2 of octahedral voids are occupied by B3+ cations. The general formula of the compound having spinel structure is
View SolutionWhat are interstitial sites ? Discuss tetrahedral and octahedral sites in close packed arrangement :
View Solution
