For the diffraction from a crystal with λ=1Å and Bragg's angle θ=60∘, then for the second order diffraction 'd' will be :
1.15 Å
0.75 Å
0.55 Å
2.1 Å
The correct Answer is:A
nλ=2dsinθ, θ=60∘,n=2
d=2×1×2×10−102×√3=1.15Å
Related Playlists
- BOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - PHYSICS157videos
NEET
- BOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - QUESTION95videos
NEET
- BOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - MOTION IN TWO AND THREE DIMENSIONEXERCISE - All Questions47videos
MOTION IN TWO AND THREE DIMENSION
- BOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEET 2020EXERCISE - All Questions45videos
NEET 2020
Similar Questions
Light is incident normally on a diffraction grating through which the first order diffraction is seen at 32∘. The second order diffraction will be seen at
View SolutionA plane wave falls on a diffraction grating with a grating constant d0 at a glancing angle α. Prove that the resulting diffraction will be the same as when the wave falls normally on a grating with a grating constant of d = d0sinα.
View SolutionA parallel beam of X-rays with a wavelenght of 1.47 Å falls at a glancing angle of 31∘3' on a face of a rocksalt crystal. Find the spacing between the atomic planes of the crystal, if the second - order diffraction maximum is observed at this angle.
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
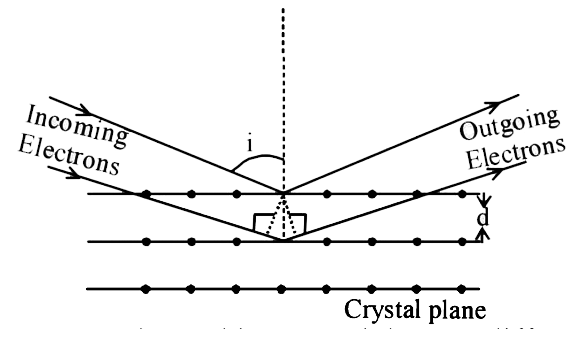
If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)View SolutionA slit of width a is illuminiated by white light. The first diffraction minimum for light of λ=6500Å is formed at θ=30∘, then the width (a) of the slit is
View SolutionX-rays are diffracted from a crystal of lattice plane spacing 2A∘.The maximum wavelength that can be diffracted is
View SolutionX-rays are diffracted from a crystal of lattice plane spacing 2A∘.The maximum wavelength that can be diffracted is
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
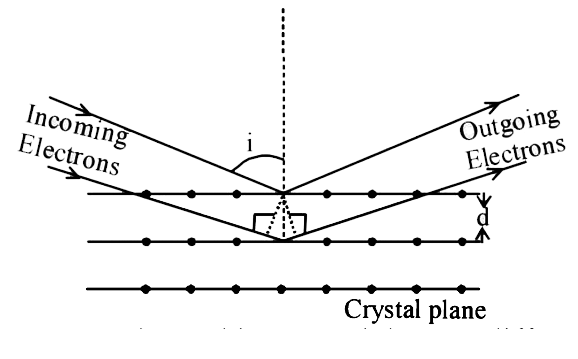
Electron accelerated by potential V are diffracted from a crystal if d=1Åandi=30∘,V should be about (h=6.6×10−34Js,me=9.1×10−31kg,e=1.6×10−19C)View SolutionCalculate λ of X-rays which give a diffraction angle 2θ=16.8∘ for crystal, if the interplanar distance in the crystal is 0.2nm and that only for the first-order diffraction is observed. Given sin8.40∘=0.146.
View SolutionWave property of electrons implies that they will show diffraction effects. Davission and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure)
_E01_233_Q01.png)
The surface of a metal is illuminated with the light of 400nm. The kinetic energy of the ejected photoelectrons was found to be 1.68eV. The work function of the metal is : (hc=1240eV−nm)View Solution


