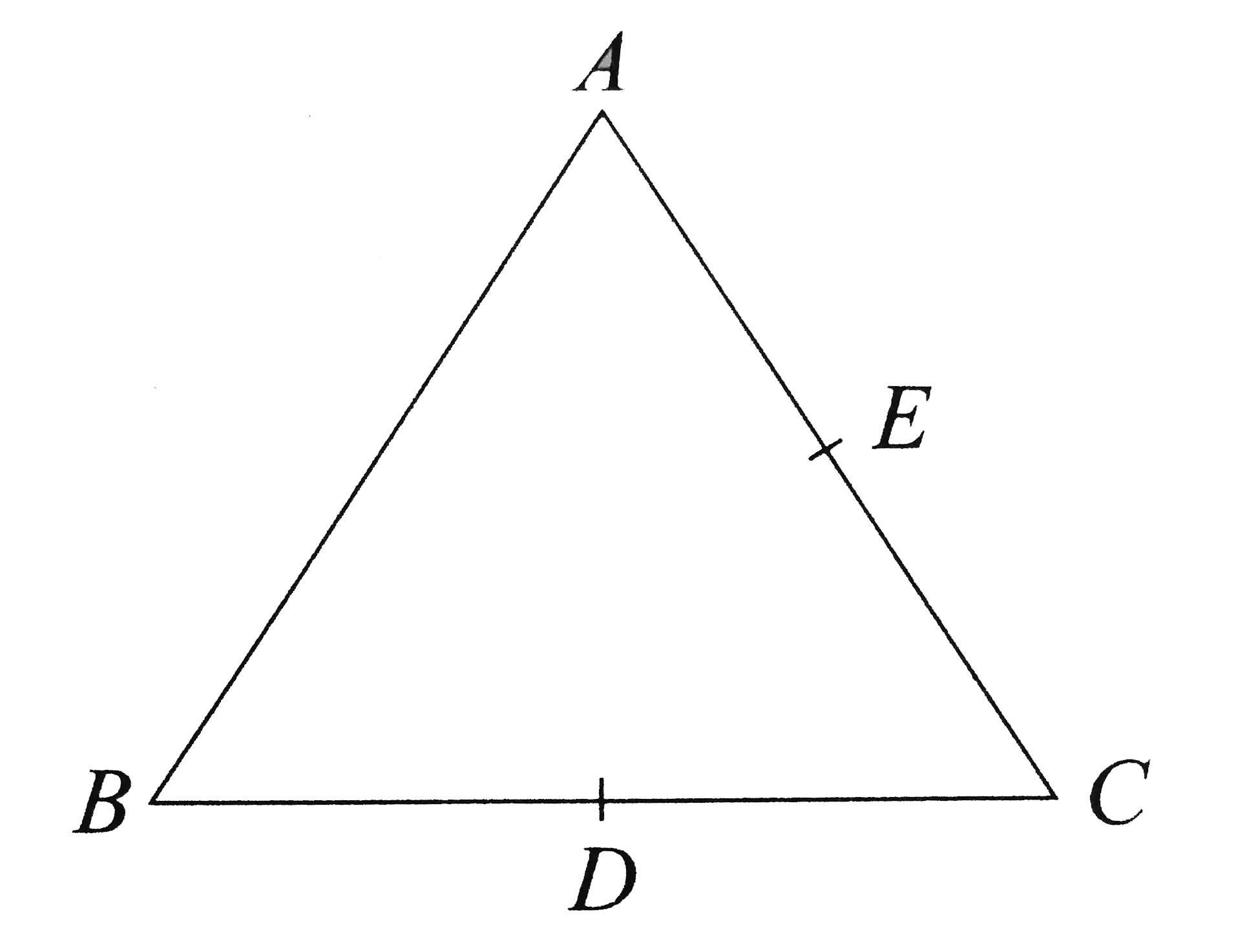
Three charges each +q, are placed at the corners of an isosceles triangle ABC of sides BC and AC, 2a D and E are the mid point of BC and CA. The work done in taking a charge Q and D to E is :

A

$\frac{3 q Q}{4 π \in_{0} a}$

B

$\frac{3 q Q}{8 π \in_{0} a}$

C

$\frac{q Q}{4 π \in_{0} a}$

D

Zero

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:D

To solve the problem of finding the work done in moving a charge $Q$ from point $D$ to point $E$ in the presence of three charges $+ q$ located at the corners of an isosceles triangle, we can follow these steps:
Step 1: Understand the Configuration
We have an isosceles triangle $A B C$ with $A B = A C = 2 a$ and $B C$ as the base. The points $D$ and $E$ are the midpoints of sides $B C$ and $A C$ respectively.
Step 2: Calculate the Potential at Points $D$ and $E$
The electric potential $V$ at a point due to a point charge is given by the formula:
$V = k \frac{q}{r}$
where $k$ is Coulomb's constant, $q$ is the charge, and $r$ is the distance from the charge to the point where the potential is being calculated.
Potential at Point $D$ :
1. The distance from charge $A$ to point $D$ is $A D = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$ .
2. The distance from charge $B$ to point $D$ is $B D = a$ .
3. The distance from charge $C$ to point $D$ is $C D = a$ .
Thus, the potential at $D$ is:
$V_{D} = k \frac{q}{A D} + k \frac{q}{B D} + k \frac{q}{C D} = k \frac{q}{a \sqrt{2}} + k \frac{q}{a} + k \frac{q}{a}$
$V_{D} = k (\frac{q}{a \sqrt{2}} + \frac{2 q}{a})$
Potential at Point $E$ :
1. The distance from charge $A$ to point $E$ is $A E = a$ .
2. The distance from charge $B$ to point $E$ is $B E = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$ .
3. The distance from charge $C$ to point $E$ is $C E = a$ .
Thus, the potential at $E$ is:
$V_{E} = k \frac{q}{A E} + k \frac{q}{B E} + k \frac{q}{C E} = k \frac{q}{a} + k \frac{q}{a \sqrt{2}} + k \frac{q}{a}$
$V_{E} = k (\frac{2 q}{a} + \frac{q}{a \sqrt{2}})$
Step 3: Compare the Potentials
From the calculations:
- $V_{D} = k (\frac{q}{a \sqrt{2}} + \frac{2 q}{a})$
- $V_{E} = k (\frac{2 q}{a} + \frac{q}{a \sqrt{2}})$
Notice that both expressions for $V_{D}$ and $V_{E}$ are equal:
$V_{D} = V_{E}$
Step 4: Calculate the Work Done
The work done $W$ in moving a charge $Q$ from point $D$ to point $E$ is given by:
$W = Q (V_{E} - V_{D})$
Since $V_{E} = V_{D}$ :
$W = Q (0) = 0$
Final Answer
The work done in taking charge $Q$ from point $D$ to point $E$ is:
$0$

|

Updated on:7/8/2024

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three charges each $+ q$ , are placed at the corners of an isosceles triangle $A B C$ of sides $B C$ and $A C, 2 a, D$ and $E$ are the mid-points of $B C$ and $C A$ . The work done in taking a charge $Q$ from $D$ to $E$ is

A $\frac{e q Q}{8 π ε_{0} a}$
B $\frac{q Q}{4 π ε_{0} a}$
Czero
D $\frac{3 q Q}{4 π ε_{0} a}$
Question 2 - Select One
Three cahrges each $+ q$ , are placed at the corners of an isosceles trinagle $A B C$ of sides $B C$ and $A C, 2 a, D$ and $E$ are the mid-points of $B C$ and $C A$ . The work done in taking a charge $Q$ from $D$ to $E$ is

A $\frac{e q Q}{4 π ε_{0} a}$
B $\frac{q Q}{4 π ε_{0} a}$
Czero
D $\frac{3 q Q}{4 π ε_{0} a}$
Question 3 - Select One
Three charges each +q, are placed at the corners of an isosceles triangle ABC of sides BC and AC, 2a D and E are the mid point of BC and CA. The work done in taking a charge Q and D to E is :
A $\frac{3 q Q}{4 π ε_{0} a}$
B $\frac{3 q Q}{8 π ε_{0} a}$
C $\frac{q Q}{4 π ε_{0} a}$
Dzero

NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)-NEET-MCQ

Home
Ask Doubt
Profile