A particle of mass M starting from rest undergoes uniform acceleration. If the speed acquired in time T is V, the power delivered to the particle is -
12MV2T2
MV2T2
12MV2T
MV2T
The correct Answer is:C
To find the power delivered to a particle of mass M that starts from rest and undergoes uniform acceleration, we can follow these steps:
1. Identify the initial conditions:
The particle starts from rest, so the initial velocity u=0.
2. Use the equation of motion to find acceleration:
The final velocity v after time T is given. Using the equation of motion:
v=u+aT
Since u=0, we have:
v=aT⟹a=vT
3. Calculate the force acting on the particle:
Using Newton's second law, the force F can be calculated as:
F=M⋅a=M⋅vT
4. Determine the displacement of the particle:
The displacement d during the time T can be calculated using the equation:
d=uT+12aT2
Again, since u=0:
d=12aT2=12(vT)T2=12vT
5. Calculate the work done on the particle:
Work done W is given by:
W=F⋅d
Substituting the values of F and d:
W=(M⋅vT)⋅(12vT)=12Mv2
6. Determine the power delivered to the particle:
Power P is defined as work done per unit time:
P=WT=12Mv2T=12Mv2T
Final Answer:
The power delivered to the particle is:
P=12Mv2T
The particle starts from rest, so the initial velocity u=0.
The final velocity v after time T is given. Using the equation of motion:
v=u+aT
Since u=0, we have:
v=aT⟹a=vT
Using Newton's second law, the force F can be calculated as:
F=M⋅a=M⋅vT
The displacement d during the time T can be calculated using the equation:
d=uT+12aT2
Again, since u=0:
d=12aT2=12(vT)T2=12vT
Work done W is given by:
W=F⋅d
Substituting the values of F and d:
W=(M⋅vT)⋅(12vT)=12Mv2
Power P is defined as work done per unit time:
P=WT=12Mv2T=12Mv2T
The power delivered to the particle is:
P=12Mv2T
Topper's Solved these Questions
- NEETBook:NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)Chapter:NEETExercise:QUESTION
Explore 95 Videos
- NEETBook:NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)Chapter:NEETExercise:MCQ
Explore 95 Videos
- NEETBook:NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)Chapter:NEETExercise:MCQ
Explore 95 Videos
- MOTION IN TWO AND THREE DIMENSIONBook:NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)Chapter:MOTION IN TWO AND THREE DIMENSIONExercise:All Questions
Explore 47 Videos
- NEET 2020Book:NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)Chapter:NEET 2020Exercise:All Questions
Explore 45 Videos
Similar Questions
A particle starts moving from rest on a straight line. Its acceleration a verses time t is shown in the figure. The speed of the particle is maximum at the instant

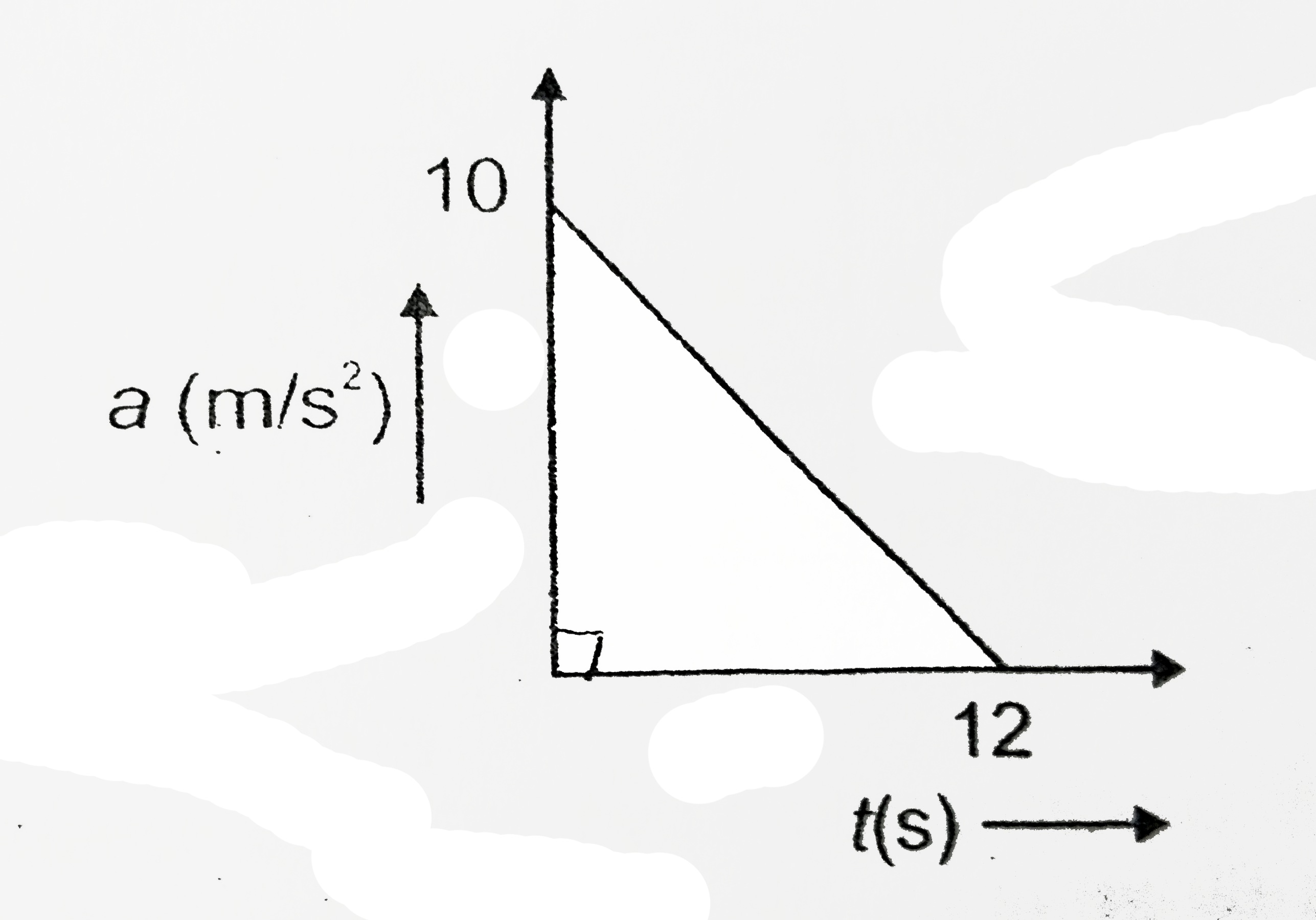
View SolutionA particle starts from rest at t=0 and undergoes an acceleration as shown in figure.
Draw the displacement-time graph of the motion of the particle during the same time interval. In both the above cases, explain the various steps.
View Solution
Knowledge Check
A particle start from rest, with uniform acceleration at time t, choose the correct option
A_2019_CBT2_E01_016_O01.png) B
B_2019_CBT2_E01_016_O02.png) C
C_2019_CBT2_E01_016_O03.png) D
D_2019_CBT2_E01_016_O04.png)
A particle starts from rest with uniform acceleration a. Its velocity after n seconds is v. The displacement of the particle in the two seconds is :
A2v(n−1)nBv(n−1)nCv(n+1)nD2v(2n+1)nA particle starts from rest and moves with acceleration a which varies with time t as a=kt where k is a costant. The displacement s of the particle at time t is
A12kt2B12at2C16at2DNone
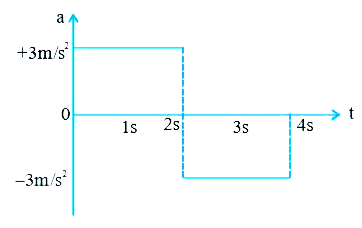
A particle starting from rest undergoes a rectilinear motion with acceleration a. The variation of a with time t is shown below. The maximum velocity attained by the particle during its motion is
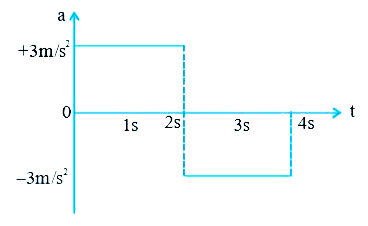
View SolutionA particle starts from rest at t=0 and undergoes an acceleration as shown in figure.
Draw the velocity-time graph of the motion of the particle during the interval from zero to 4 second.
View SolutionA particla starting from rest undergoes acceleration given by a=|t−2| m/s2 where t is time in sec. Find velocity of particle after 4 sec. is :-
View SolutionA particle of mass m is at rest. A force Facts upon it for time t. It acquires kinetic energy equal to
View SolutionA particle of mass m is released from rest and follows a particle as a function of time?
View Solution

