Twenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is: 25 (2) 30 (3) 12.5 (4) 10
30
12.5
10
25
The correct Answer is:4
Total length r+r+rθ=2θ
→θ=20−2rr ltbvrgt Therefore area of flower bed

A=12r2θ=12r220−2rr
→A=10r−r2=25−(r−5)2
∴Amax=25 (when r=5)
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:JEE Advanced Previous Year
Explore 17 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Exercise (Numerical)
Explore 20 Videos
- METHODS OF DIFFERETIATIONBook:CENGAGEChapter:METHODS OF DIFFERETIATIONExercise:Question Bank
Explore 29 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSExercise:Comprehension Type
Explore 6 Videos
Similar Questions
Twenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is: 25 (2) 30 (3) 12.5 (4) 10
View SolutionThree plots having areas 110, 130 and 190 square metres are to be subdivided into flower beds of equal size. If the breadth of a bed is 2 metre, the maximum length of a bed can be (a) 5m (b) 11m (c) 13m (d) 19m
View Solution
Knowledge Check
Twenty meters of wire is available for fencing a flower -bed in the form of a circular sector .Then the maximum area in square meters of the flower bed is
A12.5B10C25D30Shown below is the top view of a stadium. There is a badminton court at the centre. The stadium is surrounded by a jogging track. The track is semi-circular in shape at the top and the bottom of the court. The fountains converge at the centre of the respective semicircles. The jogging track has a uniform width of 2 m.
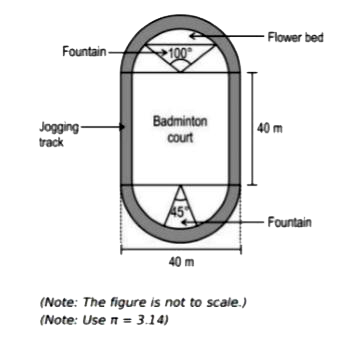
The cost of gardening is Rs 300/m2 and the area of the fountain next to the flower bed is 150 m2.
What is the cost of gardening the flower bed?ARs 39780BRs 45000CRs 59664DRs 84780
A square lawn with side 100 m long has a circular flower bed in the centre. If the area of the lawn, excluding the flower bed, is 8614 m2, the radius of the circular flower bed is (a) 21 m (b) 31 m (c) 41 m (d) None of these
View SolutionFind maximum possible area that can be enclosed by a wire of length 20cm by bending it in form of a circular sector. 10 (b) 25 (c) 30 (d) 20
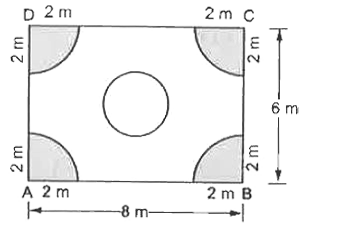
View SolutionIn each of the corners, there is a flower bed in the form of a quadrant of a circle of radius 2 m. Also, there is a flower bed in the form of a circle of radius 2 m in the middle of the plot. Find the area of the remaining plot.
View SolutionMaximum possible area that can be enclosed by a wire of length 20 cm by bending it in form of a circular sector is 10 b. 25 c. 30 d. 20
View SolutionA copper wire of length 36 m and diameter 2 mm is melted to form a sphere. The radius of the sphere (in cm) is (a) 2.5 (b) 3 (c) 3.5 (d) 4
View SolutionA square park has each side of 100 m. At each corner of the park, there is a flower bed in the form of a quadrant of radius 14 m as shown in Fig. 15.37. Find the area of the remaining part of the park (Use π=22/7) . (FIGURE)
View Solution

