A right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter. If the maximum area of the triangle is M , then the value of 32√3Mc is______
The correct Answer is:9
BC×Ce=AC×CD
therfore(BC)(CE)=x(1−x)
But BC=CE
thereBC=√x(1−x)
∴Area△=x√x−x22
or △=x3−x44
or d△2dx=3x2−4x34
If d△2dx=0 then x=34 which is the point of maxima
Hence maximum area is 3√332

Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:JEE Main Previous Year
Explore 10 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:JEE Advanced Previous Year
Explore 17 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Matrix Match Type
Explore 11 Videos
- METHODS OF DIFFERETIATIONBook:CENGAGEChapter:METHODS OF DIFFERETIATIONExercise:Question Bank
Explore 29 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSExercise:Comprehension Type
Explore 6 Videos
Similar Questions
A right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter. If the maximum area of the triangle is M , then the value of 32√3Mc is______
View SolutionOne of the legs of a right triangle is 9 cm. If the area of the triangle is 225 cm”, then the length of the other leg is
View Solution
Knowledge Check
If the perimeter of an isosceles right triangle is (6+3√2)m , then the area of the triangle is 4.5 m2 (b) 5.4 m2 (c) 9 m2 (d) 81 m2
A4.5 m2B5.4 m2C9 m2D81 m2The area of the largest triangle that can be inscribed in a semicircle of radius 6 m is
A36m2B72m2C18m2D12m2
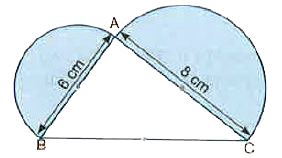
In Fig 12.58, ABC is a triangle right angled at A. Semicircles are drawn on AB and AC as diameters. Find the area of the shaded region.
View SolutionThe area of a right triangle is 6864 sq. units. If the ratio of its legs is 143:24, then the value of r is ______
View SolutionConsider a right triangle with legs of length a and b and hypotenuse of lengthc. If k denotes the area of the triangle then the value of (a+b) equals
View SolutionA triangle of maximum area is inscribed in a circle. If a side of the triangle is 20√3 then the radius of the circle is
View SolutionABC is a right-angled triangle at A. Semicircles drawn on AB, AC and BC as diameters. Find area of the shaded region.

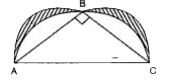
View SolutionIn the given figure, ABC is a right angled triangle with B as right angle. Three semicircles are drawn with AB, BC and AC as diameters. What is the area of the shaded portion, if the area of ΔABC is 12 square units ?
View Solution

