Using the relation 2(1−cosx)<x2,x≠0 or otherwise, prove that s∈(tanx)≥x,∀x∈[0,π4].
Video Solution
Text Solution
Give that 2(1−cosx)<x2,x≠0
To prove sin (tanx)≥x,x∈[0,π/4], let us consider
f(x)=sin(tanx )-x
f(x) =cos (tanx ) sec2x−1
=cos(tanx)−cos2xcost(2)x
sin2x1−(1)2cos2x(cost(2))x
=sin2xcos2x2cos4x>0∀x∈[0,[π/4]
Therefore f(x)>0 .Thus f(x) is an increasing function
so ,for x in [0,π/4]we have
x≥0 or f(x)≥f(0)
sin(tanx)−x≥sin(tan0)−0
sin(tanx)−x≥0
sin(tanx)≥x
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Illustration2videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise 6.110videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank29videos
METHODS OF DIFFERETIATION
- BOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If x1,x2,...,xn are real numbers, then the largest value of the expression
sinx1cosx2+sinx2cosx3+...+sinxncosx1, isAnBn2Cn4D√n2−1
Using constraint method find the relation between accelerations of 1 and 2.
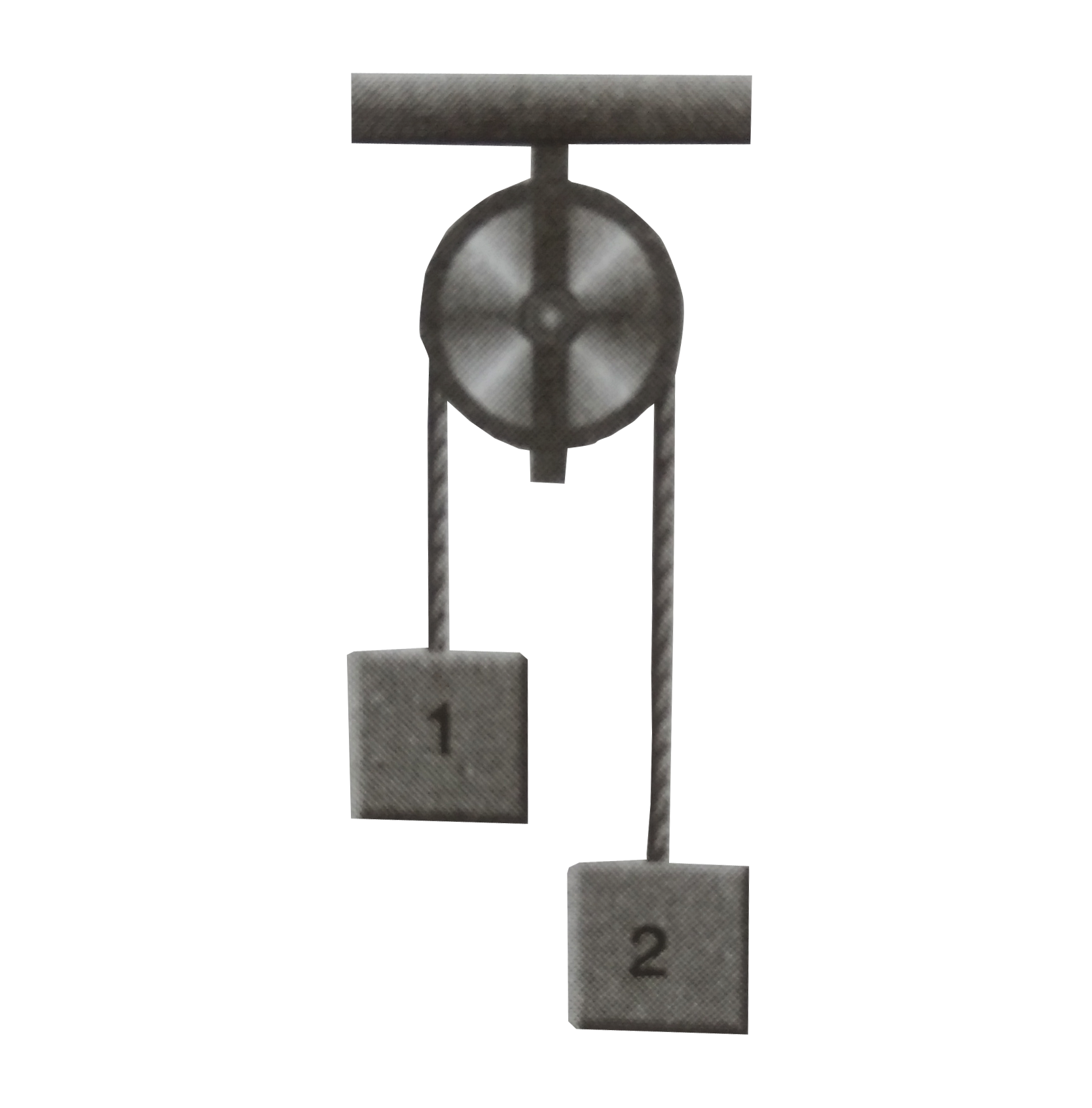
 View Solution
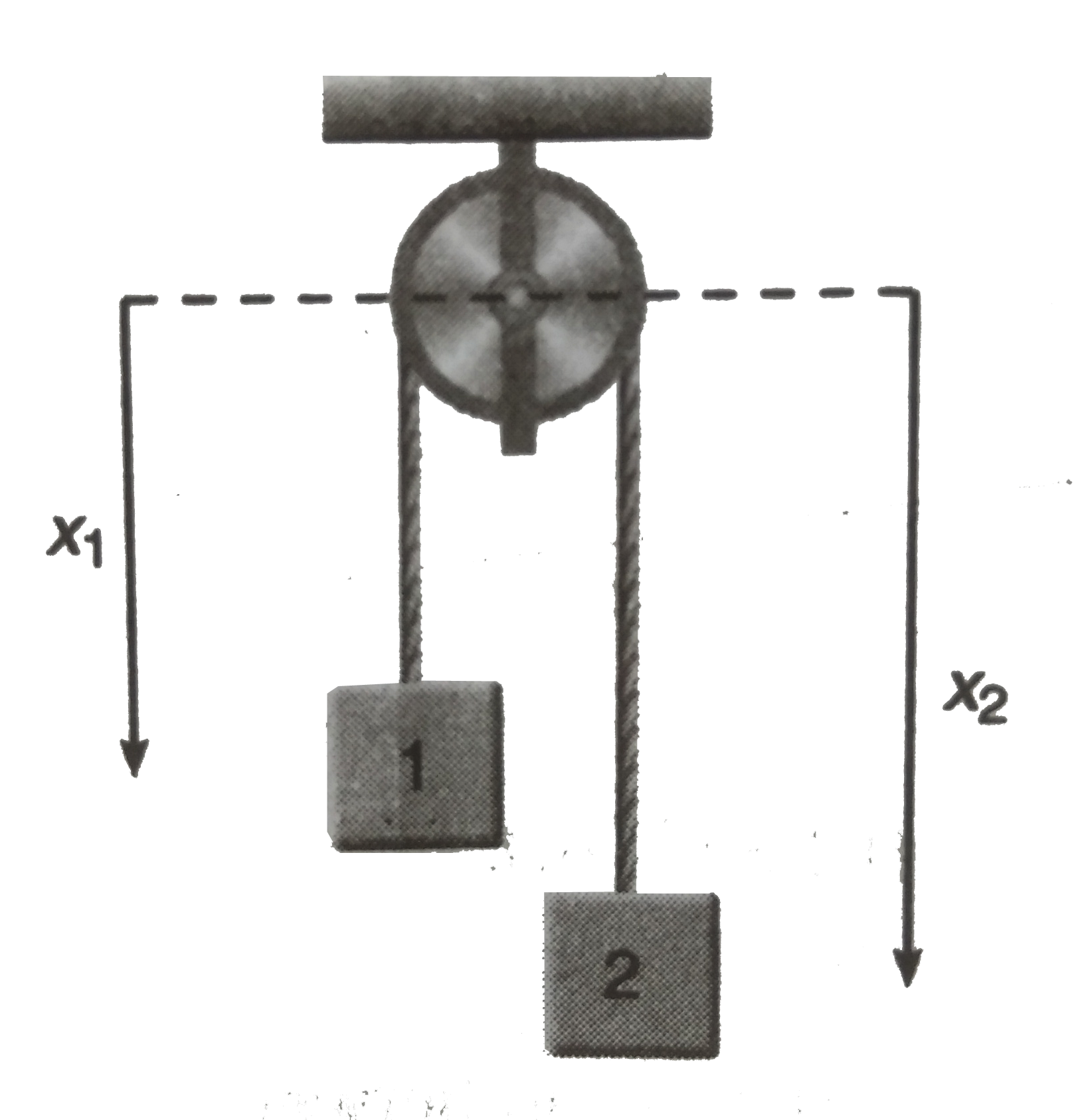
View SolutionUsing constraint method find the relation between of a1 and a2.
 View Solution
View SolutionFind the derivative of the following :
1−cosx1+cosx.View SolutionFind the differentiation of y=tan−1 ⎷1+cosx21−cosx2
View SolutionUsing contraint equation. Find the relation between a1anda2.
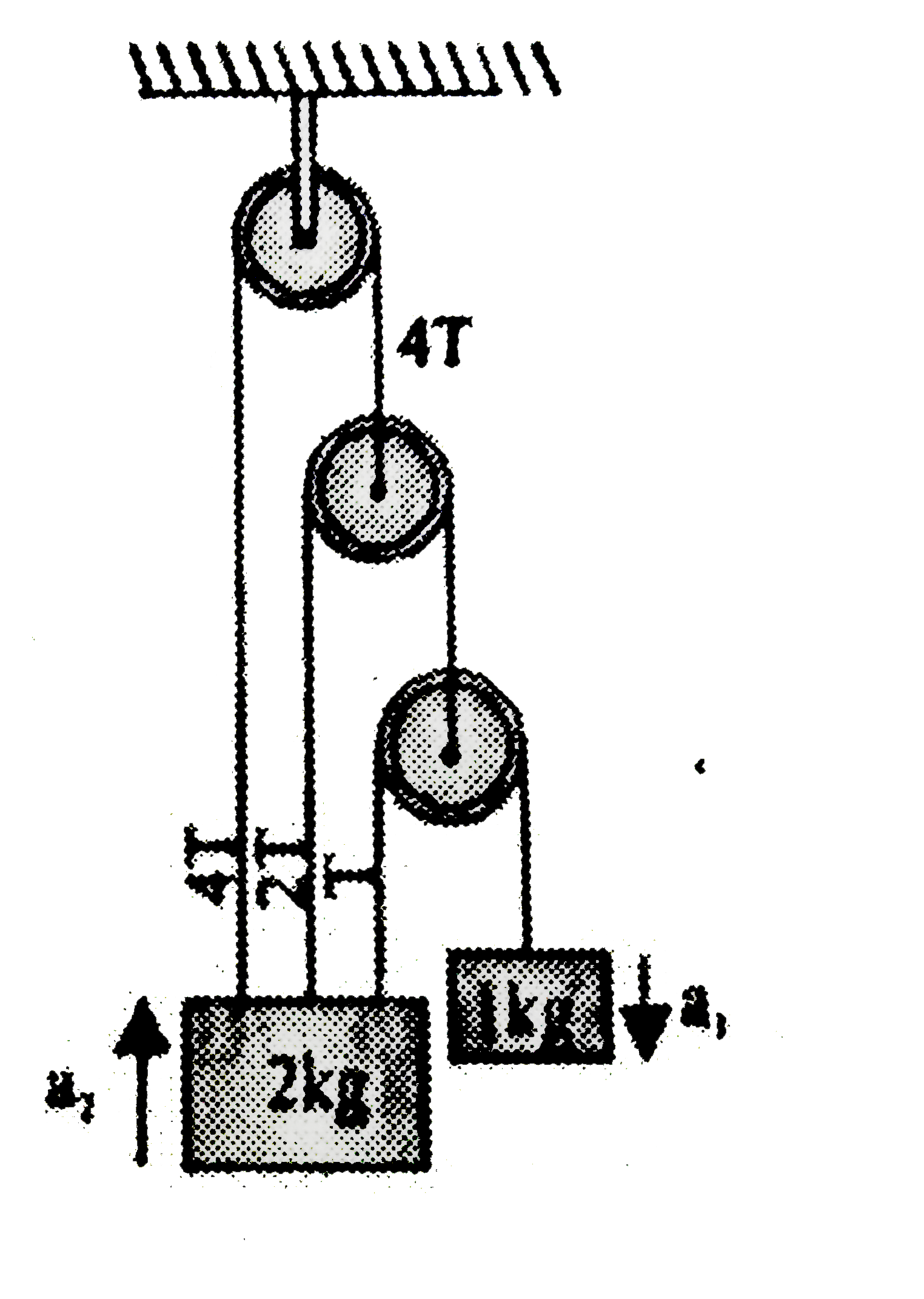 View Solution
View Solution∫sin2x(1+cosx)2dx
View Solution∫sin2x(1+cosx)2dx
View Solution

