How many ciritcal points functionf(x)=(x-1)|x-3|-4x+12 has? How many of these are points of local extrema?
f(x) =(x-1)|x-3|-4x+12
={9−x2,x<3
x2−8x+15,x≥3
∴f(x)={−2x,x≥3
22x−8,x>3
f(3)=-6,f(3)=-2
So f(x) is non differentiable at x=3
Also f(x) =0 and x=4
So , function has three critical points
Graph of the function is as shown in the following figure.

At x =3 derivation is not changing sign
So x =3 i snot a point of extrema.
At x = 0, derivation changes sign from positive to negative
So, x =0 0 is point of local maxima.
At x=3, derivative changes sign from negative to positive .
So , x=3 is point of local minima.
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Illustration
2 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise 6.1
10 Videos
- METHODS OF DIFFERETIATIONBOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank
29 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
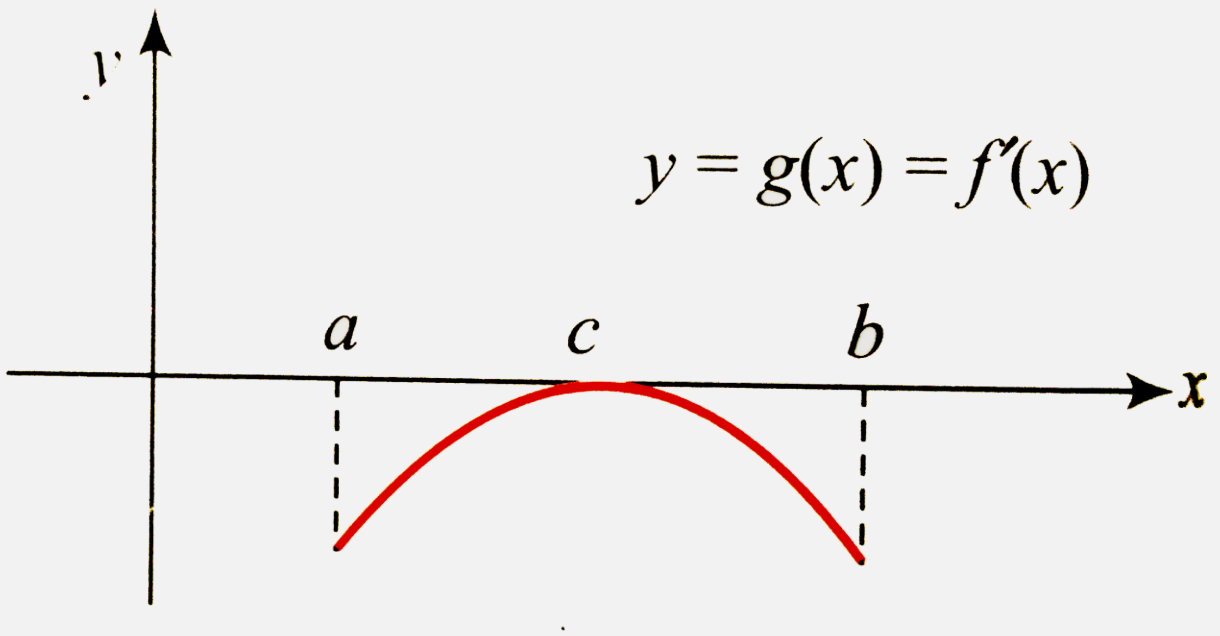
Following is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
View SolutionHow many permutations can be there with x3.y2z4? How many of these arrangements, all z are not together?
View Solution
Knowledge Check
The smallest positive integral value of a, such that the function f(x)=x4−4ax2+10 has more two local extrema, is
A1B2C4D16f(x)=2x3−3x2−12x+12 has minimum at the point
A(2,−8)B(2,8)C(−1,19)D(2,19)How many roots of the equation x−2x−1=1−2x−1 have ?
AOneBTwoCInfiniteDNone of these
Consider the function f(x)=(x−1)2(x+1)(x−2)3. What is the number of points of local minima of the function f(x)? What is the number of points of local maxima of the function f(x)?
View SolutionDiscuss the extremum of the function f(x)=(x-1)(x-2)(x-3).How many criticla points f(x) has?
View SolutionHow many points of the function f(x)=(e|x|−1)(∣x(x−1)(x−2) is not ∣∣(x2−1) differentiable?
View SolutionAt how many points is the function f(x)=[x] discontinuous?
View SolutionAt how many points is the fucntion f(x)=[x] discontinuous?
View Solution
