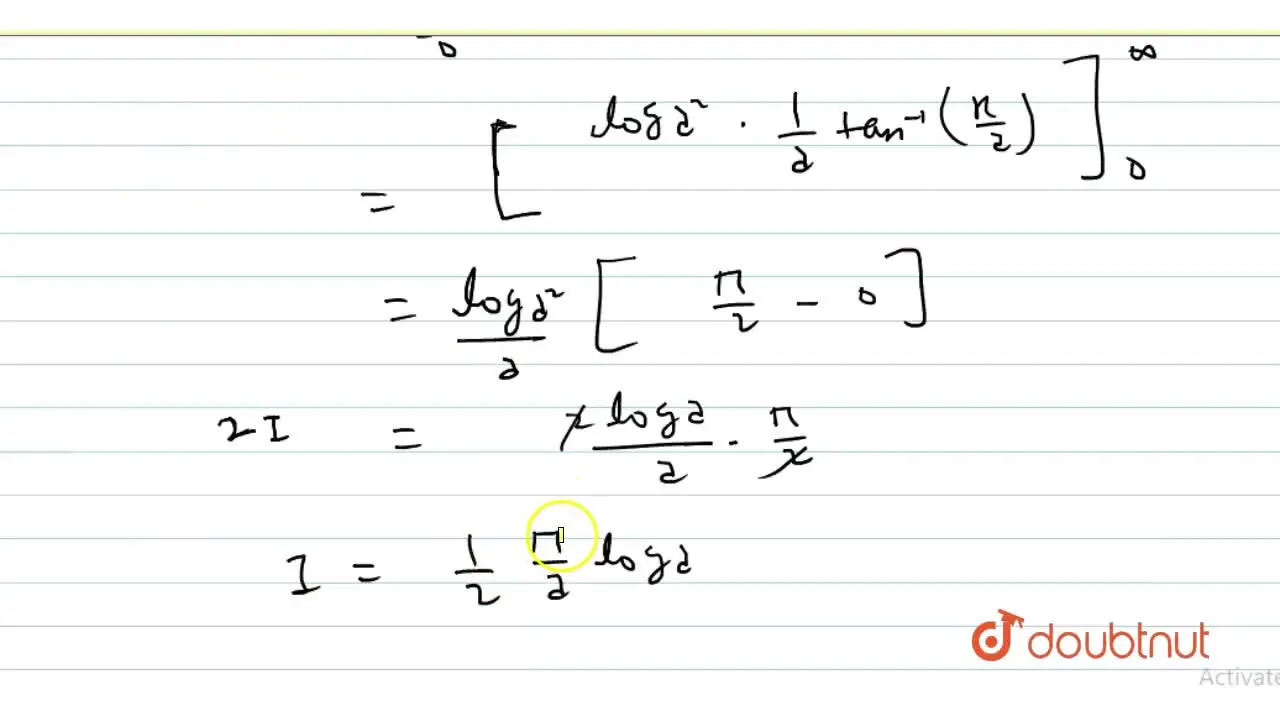The value of ∫∞0logxa2+x2dx is
A
2πlogaa
B
πloga2a
C
πloga
D
0
Video Solution
Text Solution
The correct Answer is:B
I=∫∞0logxa2+x2dx
Put x=a2y,dx=−a2y2dy
∴ I=∫0∞log(a2y)a2+a4y2(−a2y2)dy
=∫0∞(loga2−logy)a2+y2(−dy)
=log(a2)∫∞0dya2+y2−∫∞0logya2+y2dy
log(a2)1a(tan−1(ya))∞0−I
⇒ 2I=2logaa.π2
⇒ I=πloga2a
|
Updated on:21/07/2023
Similar Questions
The value of ∫∞0dxa2+x2 is equal to
View SolutionFind the value of ∫∞0xlogx(1+x2)2dx.
View SolutionThe value of ∫∞0logx1+x2dx, is
View SolutionThe value of ∫∞0x(1+x)(x2+1)dx is
View Solution" 8."int_(0)^(oo)(log x)/(1+x^(2))dx
View Solution∫∞0xlogx(1+x2)2dx=
View SolutionThe value of ∫∞0dx(x2+4)(x2+9) is
View Solution∫∞0x(1+x)(1+x2)dx
View SolutionLetA=∫∞0logx1+x3dx Then find the value of ∫∞0xlogx1+x3dx in terms of A
View Solution∫∞013+x2dx
View Solution