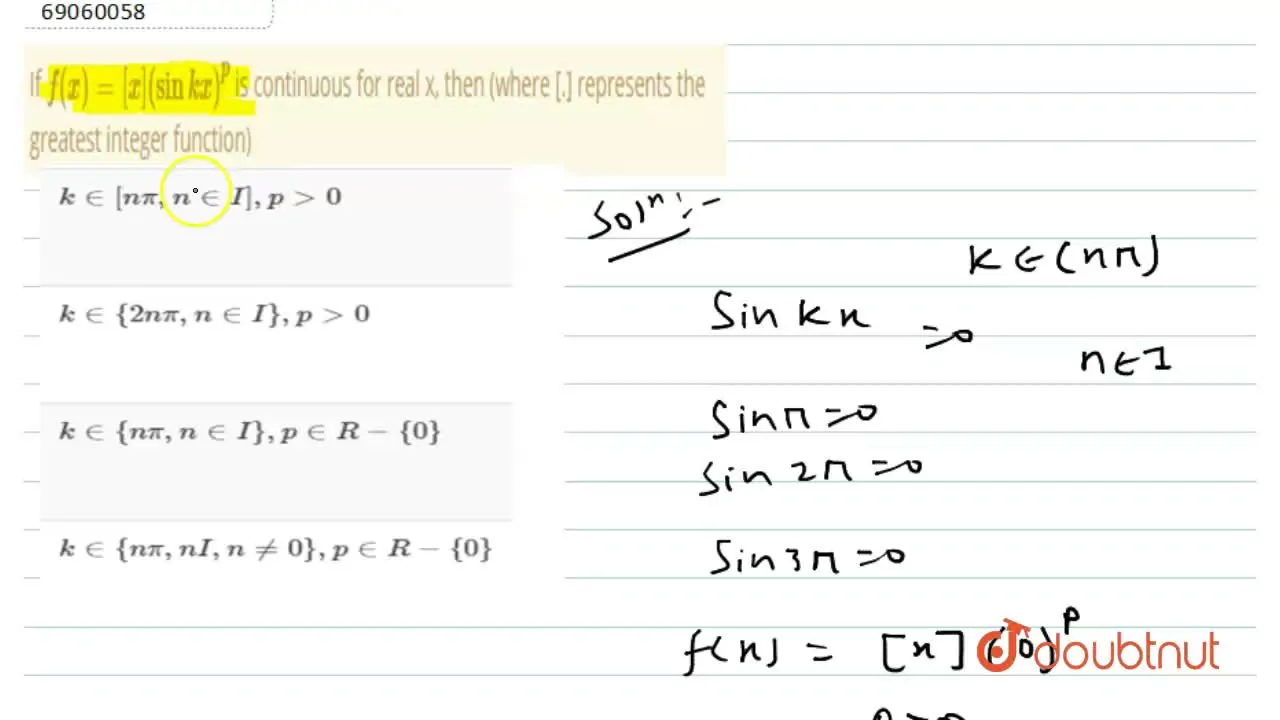If f(x)=[x](sinkx)p is continuous for real x, then (where [.] represents the greatest integer function)
k∈[nπ,n∈I],p>0
k∈{2nπ,n∈I},p>0
k∈{nπ,n∈I},p∈R−{0}
k∈{nπ,nI,n≠0},p∈R−{0}
The correct Answer is:A
f(x)=[x](sinkx)p
(sinkx)p is continuous function ∀x∈R,k∈R and p>0.[x] is discontinuous at x∈I
For k=nπ,n∈I
f(x)=[x](sin(nπx))p
limx→af(x)=0,a∈I
and f(a) = 0
So, f(x) becomes continuous for all x∈R
Related Playlists
- BOOK - CENGAGECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Multiple Correct Answer Type9videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - CENGAGECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Comprehension Type2videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises91videos
CONIC SECTIONS
- BOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
Similar Questions
Let f(x)=sin4x] then ( where [.] represents the greatest integer function ).
View SolutionEvaluate: (lim)x→0tanxx where [.] represents the greatest integer function
View SolutionIf f(x)=[2x], where [.] denotes the greatest integer function, then
View SolutionLet f(x)=−x2+x+p, where p is a real number. If g(x)=[f(x)]andg(x) is discontinuous at x=12, then p - cannot be (where [.] represents the greatest integer function)
View SolutionLet f(x) = [x] and [] represents the greatest integer function, then
View SolutionIf f(x)=|x−1|.([x]=[−x]), then (where [.] represents greatest integer function)
View SolutionThe function f(x)=cos−1⎛⎝2[|sinx|+|cosx|]sin2x+2sinx+114⎞⎠ is defined if x belongs to (where [.] represents the greatest integer function)
View SolutionFor the function f(x)=sin(π[x])×cos−1([x]), choose the correct option.
(where [.] represents the greatest integer function)View SolutionDiscuss the continuity of f(x)=[tan−1x]([.] represents the greatest integer function).
View SolutionConsider the function f(x)=cos−1([2x])+sin−1([2x]−1), then
(where [.] represents the greatest integer part function)View Solution