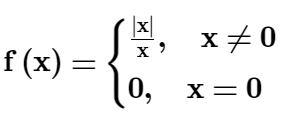If f(x)=⎧⎨⎩x+12,x<02x+34,x≥0,then[limx→0f(x)]=(where[.] denotes the greatest integer function)
12
34
does not exist
none of these
The correct Answer is:C
To solve the problem, we need to find the limit of the function f(x) as x approaches 0 from both the left and the right, and then determine the greatest integer of that limit.
1. Identify the function:
The function is defined as:
f(x)={x+12if x<02x+34if x≥0
2. Calculate the left-hand limit (LHL):
We need to find:
limx→0−f(x)
As x approaches 0 from the left, we use the first part of the function:
f(x)=x+12
Therefore:
limx→0−f(x)=limx→0−(x+12)=0+12=12
3. Calculate the right-hand limit (RHL):
Now we find:
limx→0+f(x)
As x approaches 0 from the right, we use the second part of the function:
f(x)=2x+34
Therefore:
limx→0+f(x)=limx→0+(2x+34)=2(0)+34=34
4. Determine if the limit exists:
We have:
- LHL = 12
- RHL = 34
Since LHL ≠ RHL, the limit does not exist:
limx→0f(x) does not exist.
5. Conclusion:
Since the limit does not exist, we conclude that the answer to the question is:
The limit does not exist.
Final Answer:
The greatest integer function of the limit is:
Answer: Does not exist.
The function is defined as:
f(x)={x+12if x<02x+34if x≥0
We need to find:
limx→0−f(x)
As x approaches 0 from the left, we use the first part of the function:
f(x)=x+12
Therefore:
limx→0−f(x)=limx→0−(x+12)=0+12=12
Now we find:
limx→0+f(x)
As x approaches 0 from the right, we use the second part of the function:
f(x)=2x+34
Therefore:
limx→0+f(x)=limx→0+(2x+34)=2(0)+34=34
We have:
- LHL = 12
- RHL = 34
limx→0f(x) does not exist.
Since the limit does not exist, we conclude that the answer to the question is:
The limit does not exist.
The greatest integer function of the limit is:
Answer: Does not exist.
Topper's Solved these Questions
- LIMITSBook:CENGAGEChapter:LIMITSExercise:Multiple Correct Answers Type
Explore 4 Videos
- LIMITSBook:CENGAGEChapter:LIMITSExercise:ComprehensionType
Explore 2 Videos
- LIMITSBook:CENGAGEChapter:LIMITSExercise:JEE Advanced Previous Year
Explore 7 Videos
- JEE 2019Book:CENGAGEChapter:JEE 2019Exercise:Chapter 10
Explore 9 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBook:CENGAGEChapter:LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSExercise:DPP 1.2
Explore 10 Videos
Similar Questions
Knowledge Check
limx→0x8[1x3], where [.],denotes the greatest integer function is
Aa non-zero positive real numberBa negative real numberC0Dnon-existentlimx→∞logx[x] , where [.] denotes the greatest integer function, is
A0B1C-1Dnon -existantlimx→−131x[−1x]= (where [.] denotes the greatest integer function)
A−9B−12C−6D0
The value of the limx→0xa[bx](a≠0)(where[⋅] denotes the greatest integer function) is
View Solutionf(x)=1+[cosx]x, in 0≤x≤x2 (where [.] denotes greatest integer function)
View SolutionLetf(3)=4andf'(3)=5. Then limx→3[f(x)] (where [.] denotes the greatest integer function) is
View SolutionLet f(x)={81x,x<0a[x],a∈R−{0},x≥0 (where [.] denotes the greatest integer function).
Then f(x) is
View SolutionGiven limx→0f(x)x2=2, where [.] denotes the greatest integer function, then
View Solution